Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 10.Problemas - Ex. 109

Se o anel grande, o anel pequeno e cada um dos raios pesam 500   N , 75   N e 100   N , respectivamente, determine o momento de inércia de massa da roda em relação a um eixo perpendicular à página e que passa pelo ponto A .

Passo 1

O problema pede que encontremos o momento de inércia em relação a uma eixo perpendicular à página e que passa pelo ponto A .

Primeiro, começaremos dividindo a figura em alguns segmentos:

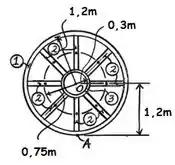
O raio da roda é:

r = 1,2 - 0,3 = 0,9   m

O centro de massa em relação ponto O :

C = 0,3 + 0,9 2 = 0,75   m

Passo 2

Agora, vamos calcular o momento de inercia com as informações que temos, em relação ao ponto O , fica:

I O = I O 1 + I O 2 + I O 3

Então:

I O = 500 9,81 1,2 2 + 8 1 1 2 100 9,81 3 2 + 100 9,81 2,5 2 + 7 5 9,81 ( 1 2 )

Calculando isso, chegamos á:

I O = 125,5   k g ⋅ m 2

Passo 3

E finalmente vamos calcular o momento de inércia em relação a um eixo paralelo perpendicular à página e que passa pelo ponto A , para isso, usamos o teorema:

I A = I O + m d 2

Sendo que a massa total é dada por:

m = 500 9,81 + 8 ⋅ 100 9,81 + 75 9,81 = 140,163   k g

E a distância é 1,2   m

Então calculando fica:

I A = 125,5 + 140,163 ⋅ 1,2 2

I A = 327,3   k g ⋅ m 2

Resposta

I O = 125,5   k g ⋅ m 2

I A = 327,3   k g ⋅ m 2

Ver Outros Exercícios desse livro