Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 5
Determine a força desenvolvida na mola exigida para manter a barra uniforme AB de 50 N ( 5 kg) em equilíbroo quando = 35º
Passo 1
Desenhando o diagrama do corpo livre e o diagrama de deslocamentos virtuais:
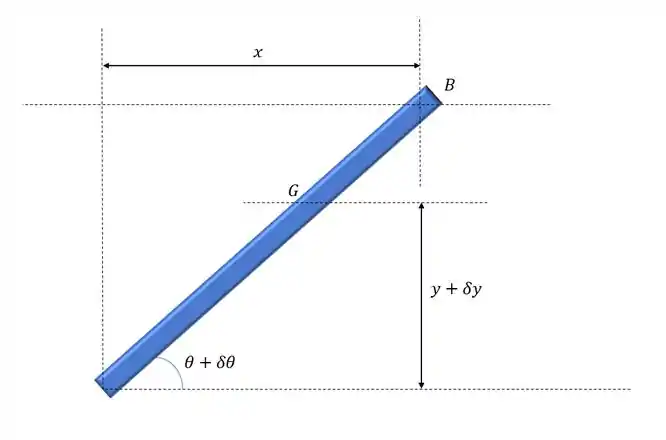
Passo 2
Vamos começar calculando as coordenadas de x e y tomando A como a origem:
Passo 3
Diferenciando essas equações para obter os deslocamentos virtuais, obtemos:
Passo 4
Com todos os dados, podemos enfim calcular o trabalho virtual:
Passo 5
Substituindo os valores de e :
Como ≠ 0:
Passo 6
Na posição de equilíbrio, :
Resposta
Exercícios de Livros Relacionados
A alça é presa a uma das engrenagens conectadas por mola, que são montadas em rolamentos fixos. A mola de rigidez k conecta dois pinos montados nas faces das engrenagens. Quando a alça está na posição
A figura mostra a vista lateral OA de uma porta de ventilador uniforme de massa m que fecha a abertura OC em uma parede vertical. A mola de rigidez k é descomprimida quando θ = 0, e a haste de luz que
Um dos requisitos críticos no projeto de uma perna artificial para um amputado é evitar que a articulação do joelho dobre sob a carga quando a perna está esticada. Como uma primeira aproximação, simul
O cilindro de massa M e raio R rola sem deslizar na superfície circular de raio 3R. Preso ao cilindro está um pequeno corpo de massa m. Determine a relação necessária entre M e m se o corpo deve ser e
Cada uma das duas engrenagens carrega uma massa excêntrica me está livre para girar no plano vertical em torno de seu rolamento. Determine os valores de θ para o equilíbrio e identifique o tipo de equ