Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 7
O mecanismo conectado por pinos é restrito em A por um pino e em B por um rolete. P = 50 N, determine o ângulo para o equilíbrio. A mola está livre quando . Despreze o peso de ambos
Passo 1
Desenhando o diagrama do corpo livre e o diagrama de deslocamentos virtuais:
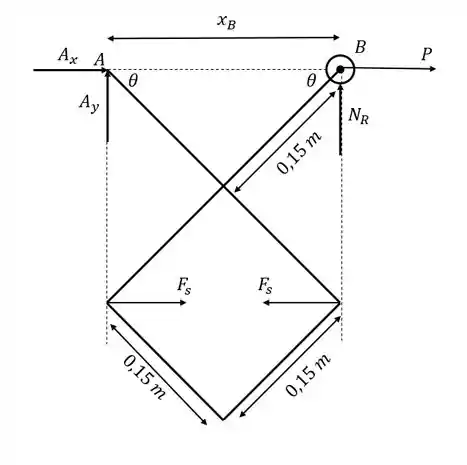
Passo 2
Vamos começar escrevendo as coordenadas de :
Passo 3
Derivando-se a expressão anterior, encontramos o deslocamento virtual:
Passo 4
Encontrando o enlongamento da mola:
Passo 5
Pela lei de Hooke, a força da mola é dada por (k=1000 N/m do enunciado):
Passo 6
Com todos os dados, podemos enfim calcular o trabalho virtual:
Resposta
Exercícios de Livros Relacionados
A lixeira tem peso W e centro de gravidade em G . Determine a força no cilindro hidráulico necessária para mantê-la na posição genérica θ .
O virabrequim está sujeito a um torque M = 50N · m . Determine a força compressiva horizontal F e faça o gráfico de F (ordenada) versus θ , (abscissa) para 0 ≤ θ ≤ 9 0 ° .
Determine o ângulo θ para haver equilíbrio e investigue a estabilidade do mecanismo nessa posição. A mola tem rigidez k = 1,5k N / m e não está deformada quando θ = 90 ° . O bloco A tem massa de 40k g
A junta articulada está sujeita à carga P . Determine a força compressiva F que ela cria sobre o cilindro em A em função de θ .
A mola conectada ao mecanismo não tem deformação quando θ = 90 ° . Determine a posição θ para haver equilíbrio e investigue a estabilidade do mecanismo nessa posição. O disco A é conectado por pino à