Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 131

Após um período de uso, uma das lâminas de um desfibrador desgasta-se, assumindo o formato mostrado na figura de massa 0,18   k g . Sabendo que os momentos de inércia da lâmina em relação aos eixos A A ' e B B ' são 0,320   g ⋅ m 2 e 0,680   g ⋅ m 2 , respectivamente, determine a a localização do eixo centroidal G G ' , b o raio de giração em relação ao eixo G G ' .

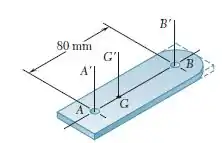
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Observe o diagrama:

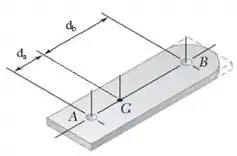
Como temos dois eixos paralelos em A A ' e B B ' , e seus respectivos momentos de inércia, vamos utilizá-los para encontrar a distância d a .

I A A ' = I G G ' + m d a 2

I B B ' = I G G ' + m d b 2

Substraindo as equações, temos:

I B B ' - I A A ' = m d b 2 - m d a 2

Sabendo que:

d b = 0,08 - d a

Temos que:

I B B ' - I A A ' = m d b 2 - 0,08 - d a 2

Resolvendo, temos que:

0,32 × 10 6 - 0,68 × 10 6 = 180 0,08 - d a 2 - d a 2

d a = 27,5   m m

Passo 2

Item b:

Com a distância do eixo A A ' , podemos calcular o momento de inércia do sistema.

I A A ' = I G G ' + m d a 2

I G G ' = I A A ' - m d a 2

I G G ' = 0,32 × 10 - 3 - 0,18 27,5 × 10 - 3 2

I G G ' = 0,1839 × 10 - 3   k g ⋅ m 2

Dividindo pela massa, temos:

k G G ' 2 = I G G ' m

k G G ' = 0,1839 × 10 - 3 0,18

k G G ' = 32   m m

Resposta

d a = 27,5   m m

k G G ' = 32   m m

Ver Outros Exercícios desse livro