Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 130

Uma peça de máquina mostrada na figura é formada por uma superfícies cônica feita por usinagem num cilindro. Para b = 1 2 h , determine o momento de inércia de massa e o raio de giração da peça da máquina com relação ao eixo y .

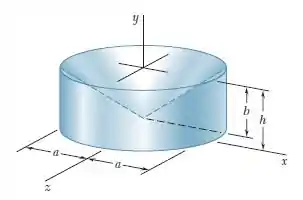
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Podemos dividir o objeto em duas partes e subtrair suas parcelas:

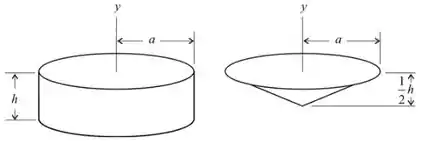
A massa do cilindro é dada por:

m c i l = ρ π a 2 h

E a massa do cone é dada por:

m c o n e = 1 3 ρ π a 2 h 2

m c o n e = 1 6 ρ π a 2 h

Portanto a massa total do objeto é dada por:

m = m c i l - m c o n e

m = ρ π a 2 h - 1 6 ρ π a 2 h

m = 5 6 ρ π a 2 h

Passo 2

O momento de inércia do cilindro em torno do eixo y é dado por:

I y c i l = 1 2 m c i l a 2

Substituindo, temos:

I y c i l = 1 2 ρ π a 2 h a 2

I y c i l = 1 2 ρ π a 4 h

O momento de inércia do cone em torno do eixo y é dado por:

I y c o n e = 3 10 m c o n e a 2

Logo:

I y c o n e = 3 10 1 6 ρ π a 2 h a 2

I y c o n e = 1 20 ρ π a 4 h

O momento de inércia total do corpo será:

I y = I y c i l - I y c o n e

I y = 1 2 ρ π a 4 h - 1 20 ρ π a 4 h

I y = 9 20 ρ π a 4 h

Podemos reorganizar e representar como:

I y = 27 50 m a 2

Onde m é a massa total.

Passo 3

Além disso, temos que:

I y = m k y 2

Substituindo, temos que:

27 50 m a 2 = m k y 2

k y 2 = 27 50 a 2

O raio de giração será:

k y = 0,735 a

Resposta

I y = 27 50 m a 2

k y = 0,735 a

Ver Outros Exercícios desse livro