Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 132

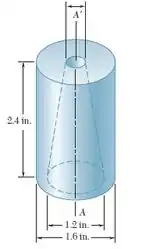
Determine o momento de inércia de massa de um componente de máquina de 4   N mostrado na figura com relação ao eixo A A ' .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos considerar o sólido como um cilindro com um cone interno. Esse cone atravessa a parte superior do cilindro. Portanto, precisamos adicionar essa parte, como representado no desenho:

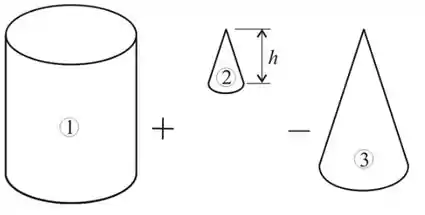
Por proporção, temos que:

h 10 = h - 60 30

Logo:

h = 30   m m

Passo 2

Com isso podemos calcular o peso das partes e o peso total.

W = ρ g ∑ V

W = ρ g π d 1 2 h 1 - π 3 d 2 h 2 - π 3 d 3 h 3

Substituindo os valores e resolvendo, encontraremos:

W = 14707   k g / m 3

As massas de cada parte são dadas por:

m 1 = 4,43   k g

m 2 = 0,012   k g

m 3 = 0,369   k g

O Momento de inércia total é dado por:

I = I 1 + I 2 - I 3

I = 1 2 m 1 a 1 2 + 3 10 m 2 a 2 2 - 3 10 m 3 a 3 2

Substituindo, os valores, temos:

I = 1 2 4,43   0,02 2 + 3 10 0,012   0,005 2 - 3 10 0,369   0,015 2

I = 9,11 × 10 - 4   k g ⋅ m 2

Resposta

I = 9,11 × 10 - 4   k g ⋅ m 2

Ver Outros Exercícios desse livro