Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 125

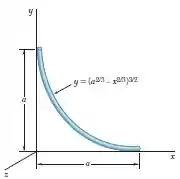
Um arame fino de aço é dobrado no formato mostrado na figura. Representado por m ' a massa por unidade de comprimento do arame, determine por integração direta o momento de inércia do arame em relação a cada um dos eixos coordenados.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos primeiramente encontrar o diferencial de massa:

d m = m d L

d m = m 1 + d x d y 2 d x

d m = m a x 1 3 d x

Intefrando, temos:

m = 3 2 m ' a

Passo 2

Para o momento de inércia em relação a x , teremos:

I x = ∫ y 2 d m

I x = ∫ 0 a a 2 3 - x 2 3 3 m ' a 1 3 x 1 3 d x  

Resolvendo, teremos:

I x = 1 4 m a 2

Passo 3

Para o momento de inércia com relação a y , teremos:

I y = ∫ x 2 d m

I y = ∫ 0 a a 2 3 - y 2 3 3 m ' a 1 3 y 1 3 d y  

Integrando, teremos:

I y = 1 4 m a 2

Portanto, em relação ao eixo z , basta somar as componentes x e y . Temos:

I z = I x + I y

I z = 1 4 m a 2 + 1 4 m a 2

I z = 1 2 m a 2

Resposta

I z = 1 2 m a 2

Ver Outros Exercícios desse livro