Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 160
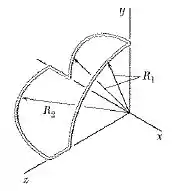
Um arame fino de alumínio com diâmetro uniforme é usado para formar a armação da figura. Representado por m’ a massa por unidade de comprimento do arame, determine os produtos de inércia , e da armação.
Passo 1
Para podermos encontrar o produto de inércia da armação, faz-se necessário saber a massa de cada componente. Note que, a questão nos oferece a massa por unidade de comprimento m’, assim podemos achar a massa em cada parte com relação a m’.
Para facilitar, vamos separar a figura em 5 partes:
1: No plano z-y.
2: Sobre o eixo z
3: No plano x-z
4: Sobre o eixo x
5: No plano x-y
Passo 2
Agora, que separamos cada parte, vamos computar a massa de cada componente. Desse modo, sabemos que:
Então,
Passo 3
Certo! Estamos quase terminando! Mas antes, observe que por causa da simetria os produtos centroides da inércia dos componentes abaixo são zero.
Além disso, temos:
Sabemos que, por meio do teorema dos eixos paralelos, segue que para os componentes 2 e 4, por causa da simetria. Restando os produtos de inercia para um quarto do círculo.
Passo 4
Para determinarmos para um quarto de um círculo, tomando como referência a imagem abaixo, temos que,
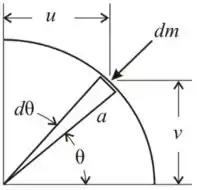
Onde
E
Onde A é a área da seção transversal do fio. Portanto:
Como,
e
Passo 5
Certo! Agora que já temos as diferenciais podemos substituir na integral. Então,
Portanto,
Por cauda da rotação de 90° dos eixos coordenados,
Passo 6
Finalmente, com as informações obtidas podemos calcular os produtos de inércia.
Assim,
E por último,