Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 147
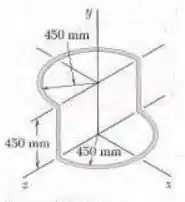
A armação mostrada na figura é formada por um arame de aço de 3 mm de diâmetro. Sabendo que a massa específica do aço é 7.850 kg/m³, determine o momento de inércia da armação em relação a cada um dos eixos coordenados.
Passo 1
Para podermos encontrar o momento de inércia da armação, faz-se necessário saber a massa de cada componente. Note que, a questão nos oferece a massa específica, assim podemos achar a massa em cada parte.
Para facilitar, vamos separar a figura em 4 partes:
1: Semicírculo da parte de baixo
2: Semicírculo da parte de cima
3: Quadrado esquerdo
4: Quadrado direito.
Passo 2
Pronto separamos a figura, agora vamos calcular a massa com as dimensões dadas. Note que:
E sabendo que:
As dimensões são as mesmas, portanto:
Do mesmo modo,
Passo 3
Com as massas de cada elemento encontrado, vamos utilizar o teorema dos eixos paralelos para podermos achar o momento de inercia.
Em relação ao eixo x, note que:
E que, como é em relação ao eixo x, então:
E sabendo que, em um quadrado:
Em um semicírculo:
Substituindo, teremos:
Obs.: Vamos utilizar o teorema do eixo paralelo no caso dois, ou seja, precisamos somar com a distância de um eixo para o outro, logo:
Assim,
Passo 4
Para o eixo y, note que:
Assim,
Passo 5
Para o eixo z, temos que:
Assim,