Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 149

Determine os produtos de inércia I x y , I y z e I z x   do aparelho de aço mostrado na figura. (A massa específica do aço é 7850 kg/m³.)

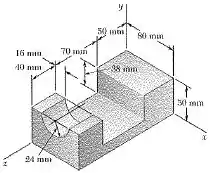
Passo 1

Antes vamos separar cada componente, de tal modo que:

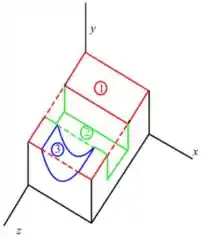
Passo 2

Agora, que separamos cada parte, vamos computar a massa de cada componente. Desse modo, sabemos que:

m = ρ V

Então,

m 1 = 7850 * 0.08 * 0.05 * 0.16 = 5.02400   k g

m 2 = 7850 * 0.08 * 0.038 * 0.07 = 1.67048   k g

m 3 = 7850 * π 2 * 0.024 2 * 0.04 = 0.28410   k g

Passo 3

Certo! Estamos quase terminando! Mas antes, observe que por causa da simetria os produtos centroides da inércia de cada componente são zero. Como também,

y - 2 = 0.05 - 0.038 2 = 0.031   m

y - 3 = 0.05 - 4 * 0.024 3 π = 0.039814   m

Assim,

Passo 4

Finalmente, com as informações obtidas podemos calcular os produtos de inércia.

Assim,

I x y = I x y 1 - I x y 2 - I x y 3 = 0 + 5.0240 - 0 + 2.0714 - 0 + 4.524 * 10 - 3

I x y = 2.50 * 10 - 3 k g * m 2

Como também,

I y z = I y z 1 - I y z 2 - I y z 3 = 0 + 10.0480 - 0 + 4.4017 - 0 + 1.5836 * 10 - 3

I y z =   4.06 * 10 - 3 k g * m 2

E por último,

I z x = I z x 1 - I z x 2 - I z x 3 = 0 + 16.0768 - 0 + 5.6796 - 0 + 1.5910 * 10 - 3

I z x = 8.81 * 10 - 3 k g * m 2

Resposta

I x y = 2.50 * 10 - 3 k g * m 2

I y z =   4.06 * 10 - 3 k g * m 2

I z x = 8.81 * 10 - 3 k g * m 2

Ver Outros Exercícios desse livro