Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 158

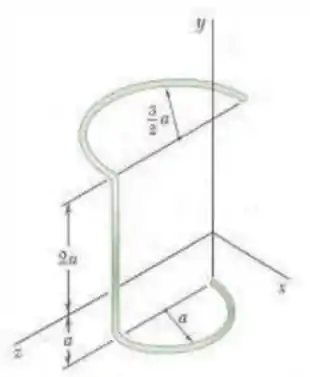
Um arame de latão com peso por unidade de comprimento w é usado para formar a armação mostrada na figura. Determine os produtos de inércia I x y , I y z   e   I z x da armação.

Passo 1

Vamos dividir nossa armação em 3 partes: a superior de raio 1.5 a , a de altura 3 a e a de raio a . Assim, calculando as suas respectivas massas vamos encontrar

m 1 = W g ⋅ π ⋅ 3 a 2 = 3 2 ⋅ π W a g

m 2 = w g ⋅ 3 a

m 3 = w g ⋅ π ⋅ a

Devido a simetria temos que os produtos de inércia I x ' y ' - ,     I y ' z ' -   e   I z ' x ' - são iguais a zero.

Passo 2

Com os dados acima podemos construir a seguinte tabela

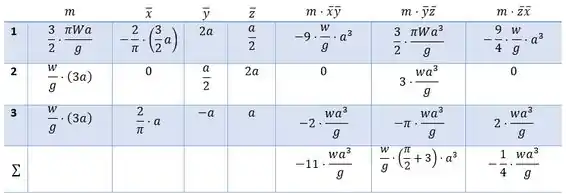
Assim teremos

I x y = ∑ I x ' y ' - + m x - y - → I x y = - 11 ⋅ w g ⋅ a 3

I y z = ∑ I y ' z ' - + m z - y - → I y z = 1 2 ⋅ w g ⋅ a 3 ⋅ π + b

I z x = ∑ I x ' z ' - + m z - x - → I z x = - 1 4 ⋅ w g ⋅ a 3

Resposta

I x y = - 11 ⋅ w g ⋅ a 3

I y z = 1 2 ⋅ w g ⋅ a 3 ⋅ π + b

I z x = - 1 4 ⋅ w g ⋅ a 3

Ver Outros Exercícios desse livro