Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 127

A figura mostra a seção transversal de uma polia plana fundida. Determine seu momento de inércia de massa e seu raio de giração em relação ao eixo A A ' . (A massa específica do latão é 8.650   k g / m 3 e a massa específica do policarbeoneto reforçado em fibra é 1.250   k g / m 3 .)

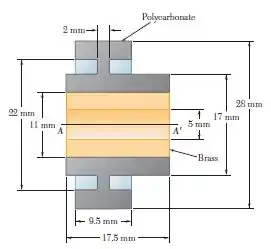
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos dividir o sistema em 4 partes:

  1. A bucha de latão.
  2. O primeiro diâmetro de 11   m m até 17   m m , com espessura 17,5   m m .
  3. Segundo diâmetro de 17   m m a 22   m m e espessura de 2   m m .
  4. Um último diâmetro de 22   m m a 28   m m e espessura de 9,5   m m .

Agora, vamos calcular, individualmente, o momento de inércia em relação ao eixo A A ' , e também a sua massa individual.

Temos que:

I A A ' = 1 2 m d e x t 2 2 - 1 2 m d i n t 2 2

Substituindo m , temos:

I A A ' = 1 8 ρ t π 4 d e x t 2 d e x t 2 - ρ t π 4 d i n t 2 d i n t 2

I A A ' = 1 8 ρ t π 4 d e x t 4 - d i n t 4

I A A ' = 1 8 ρ t π 4 d e x t 2 - d i n t 2 d e x t 2 + d i n t 2

I A A ' = 1 8 m d e x t 2 + d i n t 2

E:

m = ρ V

m = ρ t π 4 d e x t 2 - d i n t 2

Passo 2

Usando as equações e as respectivas divisões, temos:

m 1 = 8650 0,0175 0,011 2 - 0,005 2

m 1 = 11,4134   g

m 2 = 1250 0,0175 0,017 2 - 0,011 2

m 2 = 2,8863   g

m 3 = 1250 0,002 0,022 2 - 0,017 2

m 3 = 0,38288   g

m 4 = 1250 0,0095 0,028 2 - 0,022 2

m 4 = 2,7980   g

A massa total é dada por:

m = ∑ m i

m = 17,4806   g

Passo 3

Para os momentos de inércia, temos:

I   A A ' = 1 8 11,4134 0,011 2 + 0,005 2

I 1 ,     A A ' = 208,29 ⋅ 10 - 9

I 2 ,     A A ' = 1 8 2,8863 0,017 2 + 0,011 2

I 2 ,     A A ' = 147,92 ⋅ 10 - 9

I 3 ,     A A ' = 1 8 0,38288 0,022 2 + 0,017 2

I 3 ,     A A ' = 37 ⋅ 10 - 9

I 4 ,     A A ' = 1 8 2,798 0,028 2 + 0,022 2

I 4 ,     A A ' = 443,48 ⋅ 10 - 9

O momento de inércia total é dado por:

I A A ' = ∑ I i , A A '

I A A ' = 837 ⋅ 10 - 9   k g ⋅ m 2

Passo 4

O raio de giração é dado pela equação:

k A A ' 2 = ∑ I i , A A ' ∑ m i

k A A ' 2 = 4,788 ⋅ 10 - 5   m 2

k A A ' = 6,92   m m

Resposta

I A A ' = 837 ⋅ 10 - 9   k g ⋅ m 2

k A A ' = 6,92   m m

Ver Outros Exercícios desse livro