Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 170

Para a armação de arame do problema 9.148 , determine o momento de inércia de massa da armação em relação ao eixo que passa pela origem caracterizado pelo vetor unitário λ = - 3 i - 6 j + 2 k 7

Passo 1

O problema descrito no enunciado trás consigo a seguinte armação

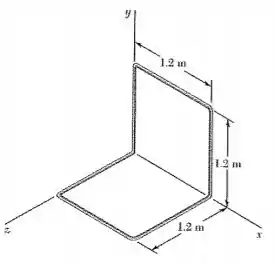
Cada aresta da nossa armação vamos denominar como um elemento e, assim, calculando suas respectivas massas vamos obter

m = m L ⋅ L = 0.056 k g m ⋅ 1.2 m = 0.0672 k g

Por conta da simetria vamos ter que os produtos inerciais I x ' y ' - ,   I y ' z ' -   e   I z ' x ' - são iguais a 0. Além disso podemos inferir que

x 1 - = x 6 - = 0 ,     y 4 - = y 5 - = y 6 - = 0   e   z 1 - = z 2 - = z 3 - = 0    

Então teremos

I x y = ∑ (   I x ' y ' - + m ⋅ x - ⋅ y - ) = m   ⋅ x 2 - ⋅ y 2 - + m ⋅ x 3 - ⋅ y 3 -

→ I x y = 2 ⋅ 0.672 k g ⋅ 0.6 m ⋅ 1.2 m = 0.096768 k g ⋅ m 2

I y z = ∑ (   I y ' z ' - + m ⋅ y - ⋅ z - ) = 0

I z x = ∑ (   I z ' x ' - + m ⋅ x - ⋅ z - ) = m ⋅ z 4 - ⋅ x 4 - + m ⋅ z 5 - ⋅ x 5 -

I z x = 2 ⋅ 0.672 k g ⋅ 0.6 m ⋅ 1.2 m = 0.096768 k g ⋅ m 2

Passo 2

Da resolução do problema 148 temos que

I x = 0.32258   k g ⋅ m 2

I y = I z = 0.41933   k g ⋅ m 2

A equação que vai nos fornecer o momento de inércia que desejamos é dada por

I o l = I x ⋅ λ x 2 + I y ⋅ λ y 2 - 2 I x y ⋅ λ x ⋅ λ y - 2 I y z ⋅ λ y ⋅ λ z - 2 I z x ⋅ λ z ⋅ λ x

I o l = 0.32258 ⋅ - 3 7 2 + 0.41933 ⋅ - 6 7 2 + 0.41933 ⋅ 2 7 2 - 2 ⋅ 0.096768 ⋅ - 3 7 ⋅ - 6 7   - 2 ⋅ 0.096768 ⋅ 2 7 ⋅ - 3 7   k g ⋅ m 2

I o l = 0.354 k g ⋅ m 2

Resposta

I o l = 0.354 k g ⋅ m 2

Ver Outros Exercícios desse livro