Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 166

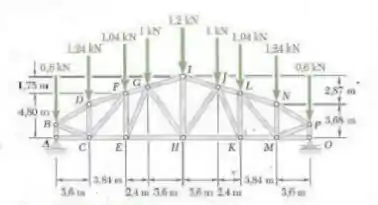
A treliça mostrada na figura foi projetada para suportar um telhado de um supermercado. Para o carregamento dado, determine a força no elemento F G ,   E G   e   E H .

Passo 1

Desejamos encontrar os valores das forças nos elementos dados e para isso vamos precisar primeiramente calcular as reações de apoio e que serão bastante simples. Nesse caso, por conta da simetria teremos

A = O = 0.6 + 1.24 + 1.04 + 1 + 1.2 + 0.6 + 1.24 + 1.04 + 1 + 1.2 2 = 4.48 k N  

Agora, pelo método das seções vamos descobrir o valor das forças desejadas pelo enunciado traçando uma seção através dos membros F G , E G   e   E H . I n c l i n a ç ã o   F G = I n c l i n a ç ã o   F I = 1.75 6

I n c l i n a ç ã o   E G = 5.5 2.4

Passo 2

Aplicando as condições de equilíbrio para o problema vamos ter

∑ M e = 0 →

0.6 k N ⋅ 7.44 m + 1.24 k N ⋅ 3.84 m - 4.48 k N ⋅ 7.44 m - 6 6.25 F f g ⋅ 4.8 m = 0

F f g = - 5.23 k N

∑ M g = 0 → F E H ⋅ 5.5 m + 0.6 k N ⋅ 9.84 m + 1.24 k N ⋅ 6.24 m + 1.04 k N ⋅ 2.4 m - 4.48 k N ⋅ 9.84 m = 0

F E H = 5.08 k N

∑ F y = 0 → 5.5 6.001 ⋅ F E G + 1.75 6.25 ⋅ - 5.23 k N + 4.48 k N - 0.6 k N - 1.24 k N - 1.04 k N = 0

F E G = - 0.1476 k N

Resposta

F f g = 5.23 k N   c o m p r e s s ã o

F e h = 5.08 k N   t r a ç ã o

F e g = 0.1476 k N   c o m p r e s s ã o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se cada membro da treliça espacial pode sustentar uma força máxima de 600N sob compressão e 800N sob tração, determine a maior força F que a treliça pode sustentar.
Determine a força nos membros E F , D F , C F e C D da treliça espacial e indique se os membros estão sob tração ou compressão.
Determine as componentes horizontal e vertical da reação no pino C .
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão.
A treliça usada para sustentar um balcão está sujeita às cargas mostradas. Considere cada nó como um pino e determine a força em cada membro. Indique se os membros estão sob tração ou compressão. Faça