Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 1
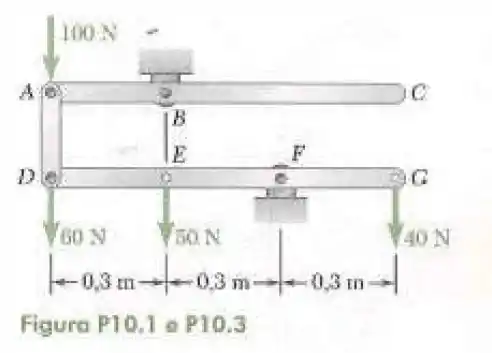
- Determine a força vertical que deve ser aplicada em para se manter o equilíbrio do sistema articulado.
Passo 1
Vamos considerar que a barra desloca de um ângulo igual a , logo:
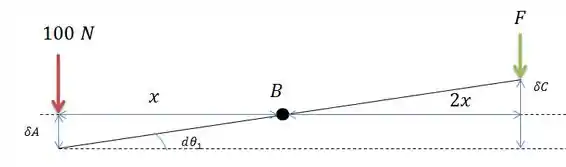
Por semelhança de triângulos conseguimos ver que:
E por estarem conectados na mesma barra vemos que:
Passo 2
Agora transferindo para a barra de baixo e considerando que ele faz um ângulo com a horizontal igual a nós vemos que:
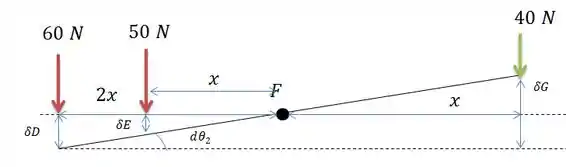
Por semelhança de triângulos vemos que:
Dessa forma vemos que
Ou:
Passo 3
Agora vamos aplicar a teoria de trabalhos virtuais que nos diz que:
Pois com a força em para baixo a distância virtual tende a diminuir (trabalho positivo) e como tende a aumentar então o trabalho feito pela força de é negativo. E o mesmo raciocínio se transfere para a barra de baixo onde e tendem a aumentar com as forças nesses pontos e a diminuir.
Com sentido para baixo mesmo.
Resposta
Exercícios de Livros Relacionados
Determine o movimento horizontal do nó D se o comprimento do elemento BF é aumentado em 1.5 in.(Ver dica para o Problema 10.57.)
Deduza uma expressão para a eficiência mecânica do macaco discutido na Seção 8.6. Mostre que, se o macaco tem que ser autotravante, a eficiência mecânica não pode exceder 1 2 .
Usando o método do trabalho virtual, determine separadamente a força e o binário que representa a reação em H.
9. Sabendo que a linha de ação da força Q passa pelo ponto C , deduza uma expressão para a intensidade de Q necessária para se manter o equilíbrio.