Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 159

A armação mostrada na figura é formada por um arame de alumínio de 1.5 m m de espessura. Sabendo que a massa específica do alumínio é 2.700 N / m m 3 , determine os produtos de inércia I x y , I y z   e   I z x da armação.

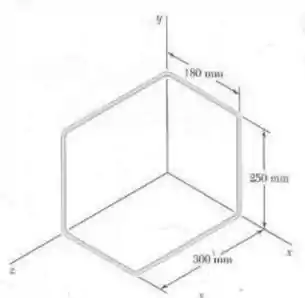
Passo 1

Vamos dividir cada aresta da nossa armação como um pedaço a ser calculador no nosso problema. Dessa forma, calculemos a massa de cada parte

m 1 = m 4 = 2800 ⋅ π 4 ⋅ 0.0015 2 ⋅ 0.25 ≈ 1.237 ⋅ 10 - 3   k g

m 2 = m 5 = 2800 ⋅ π 4 ⋅ 0.0015 2 ⋅ 0.18 ≈ 0.89064 ⋅ 10 - 3   k g

m 3 = m 6 = 2800 ⋅ π 4 ⋅ 0.0015 2 ⋅ 0.3 ≈ 1.4844 ⋅ 10 - 3   k g

Devido a simetria temos que os produtos de inércia I x ' y ' - ,     I y ' z ' -   e   I z ' x ' - são iguais a zero.

Passo 2

Com os dados acima podemos construir a seguinte tabela

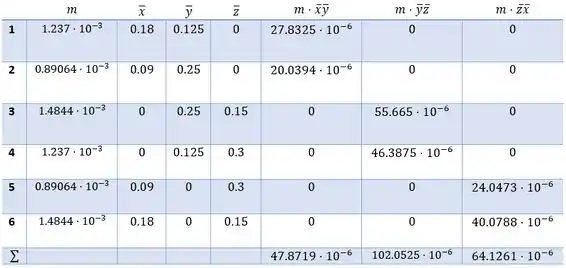
Assim, teremos

I x y = ∑ I x ' y ' - + m x - y - → I x y = 47.9 ⋅ 10 - 6   k g ⋅ m 2

I y z = ∑ I y ' z ' - + m z - y - → I y z = 102.1 ⋅ 10 - 6   k g ⋅ m 2

I z x = ∑ I x ' z ' - + m z - x - → I z x = 64 . 1 ⋅ 10 - 6   k g ⋅ m 2

Resposta

I x y = 47.9 ⋅ 10 - 6   k g ⋅ m 2

I y z = 102.1 ⋅ 10 - 6   k g ⋅ m 2

I z x = 64.1 ⋅ 10 - 6   k g ⋅ m 2

Ver Outros Exercícios desse livro