Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 163

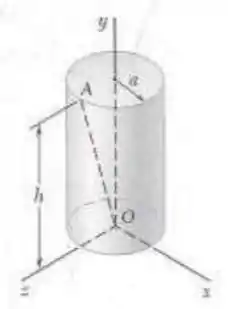
O cilindro circular homogêneo mostrado na figura tem massa m . Determine o momento de inércia do cilindro em relação à linha que liga a origem O e o ponto A localizado sobre o perímetro da superfície superior do cilindro.

Passo 1

O livro trás uma imagem que nos auxiliará muito na resolução que é

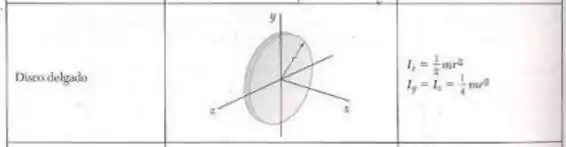
Assim, temos que

I y = 1 2 ⋅ m a 2

Usando o teorema dos eixos paralelos vamos ter

I x = I z = 1 12 ⋅ m ⋅ 3 a 2 + h 2 + m ⋅ h 2 2 = 1 12 ⋅ m ⋅ 3 a 2 + 4 h 2

Pela simetria do problema vamos ter

I x y = I y z = I z x = 0

Por conveniência vamos adotar que o ponto A está no plano x y   . Então,

λ O A = 1 h 2 + a 2 ⋅ h j + a k

Como os produtos de inércia são iguais a zero nossa equação se reduz a

I O A = I x ⋅ λ x 2 + I y ⋅ λ y 2 + I z ⋅ λ z 2

I O A = 1 2 ⋅ m a 2 ⋅ h h 2 + a 2 2 + 1 12 ⋅ m ⋅ 3 a 2 + 4 h 2 ⋅ a h 2 + a 2 2

I O A = 1 12 ⋅ m a 2 ⋅ 10 h 2 + 3 a 2 h 2 + a 2

Resposta

I O A = 1 12 ⋅ m a 2 ⋅ 10 h 2 + 3 a 2 h 2 + a 2

Ver Outros Exercícios desse livro