Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 162

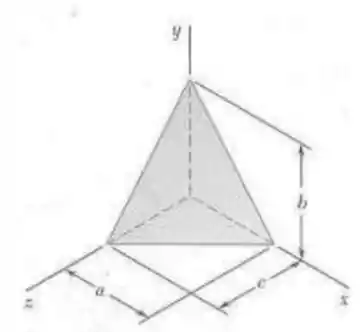
Para o tetraedro homogêneo de massa m mostrado na figura, a determine por integração direta o produto de inércia I z x ,   b deduza I y z e I x y dos resultados obtidos no item a .

Passo 1

Para resolver esse problema vamos imaginar que dividimos o nosso tetraedro em várias fatias verticais que apresentam espessura d z . Então podemos fazer

x = - a c ⋅ z + a = a ⋅ 1 - z c

y = - b c ⋅ z + b = b ⋅ 1 - z c

A massa d m da laje é

d m = ρ ⋅ d V = ρ ⋅ 1 2 ⋅ x y   d z = ρ a b 2 ⋅ 1 - z c 2 d z

Então nosso m vai ser a integral definida de 0 a c disso tudo. Dessa forma obteremos

m = 1 6 ⋅ ρ a b c

Agora, tomando o teorema dos eixos paralelos para os infinitesimais teremos

d I z x = d I z ' x ' - + Z e l - ⋅ X e l - d m   e   d I z ' x ' - = 0   p e l a   s i m e t r i a

Além disso temos

Z e l - = z ,     X E L - = x 3 = a 3 ⋅ 1 - z c

Então, mais uma vez integrando de forma definida de 0   a   C   vamos obter

I z x = ∫ d I z x = m a c ⋅ z 2 2 - z 3 c + 3 4 ⋅ z 4 c 2 - 1 5 ⋅ z 5 c 3 0 c = 1 20 ⋅ m a c

Passo 2

Agora que fizemos todas essas contas vamos aproveitar a simetria do corpo para acharmos I x y e I y z que podem ser deduzidos considerando uma permutação circular de x , y , z e a , b , c . Portanto,

I x y = 1 20 ⋅ m a b

I y z = 1 20 ⋅ m b c

Resposta

a   I z x = 1 20 ⋅ m a c

b I x y = 1 20 ⋅ m a b ,     I y z = 1 20 ⋅ m b c

Ver Outros Exercícios desse livro