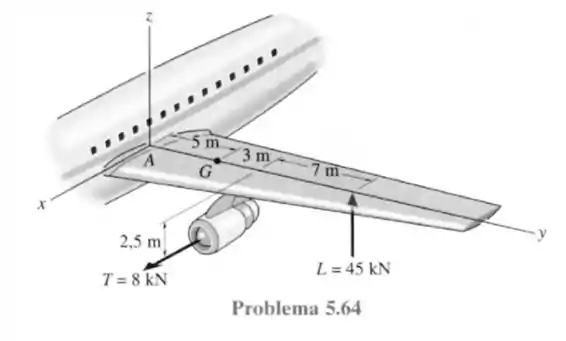
64- As asas de um avião a jato estão sujeitas cada uma a um arranque de de sua turbina e a força de elevação resultante . Se a massa de uma asa é de e seu centro de massa está em , determine os componentes de reação no ponto , local onde a asa é fixada na fuselagem.
Passo 1
Fala meus engenheiro aeronáutico, psicologicamente pronto para mais uma?
Pode-se considerar a asa do avião como um elemento engastado e isso faz com que ele resista a força nos três eixos e ao torque também. Fazendo com que tenha o seguinte sistema de forças abaixo.
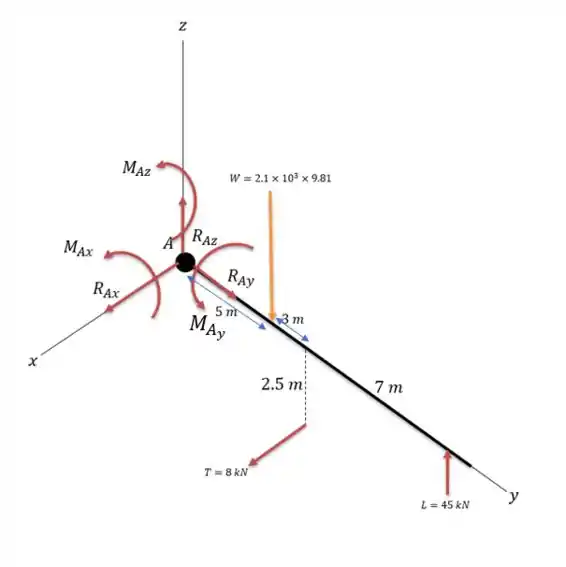
Peço que tenha a boa vontade de entender que em temos o centro da resistência de todos os momentos e reações da asa do nosso avião. Considerando como positivo o torque no sentido anti-horário.
E perceba que , já que .
Fazendo a somatória das forças em temos:
Isso significa que o sentido da força está ao contrário ao do desenhado no sistema, porém o módulo é de .
Fazendo a somatória das forças em temos:
Como a asa do avião não está sendo sobrecarregada no eixo então não resistem em reação nesse eixo.
E a somatória das forças em :
O módulo dessa força é de ainda assim
Passo 2
Agora chegou a hora de analisar os momentos resistentes na asa. Sabendo que o sentido anti-horário é positivo para:
Começando com a força de que gera momento na distância de , a força tem sentido no eixo enquanto tem uma distância no eixo , logo o momento é em , logo (para sentido anti-horário sendo positivo):
A força de com sentido no eixo também gera momento no pedaço da asa de tamanho de com direção no eixo , logo vamos calcular o momento em . Logo para o sentido anti-horário sendo o positivo temos:
Agora só falta o momento em , e elas são causadas pelas forças peso e (que tem em sentido em ) no eixo , o cálculo delas encontra-se abaixo:
Isso nos diz que o sentido da reação do momento em está no sentido horário.