Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 39

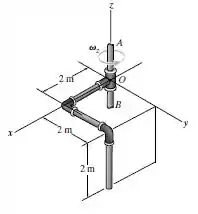
A barra dobrada tem uma massa por unidade de comprimento de 6   k g / m , e seus momentos e produtos de inércia foram calculados no Problema 21.9 . Se o eixo A B gira com uma velocidade angular constante ω 2 = 6   r a d / s , determine a quantidade de movimento angular da barra em relação ao ponto O e a energia cinética da barra.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos que:

ω = 6 k   r a d / s

Logo:

ω x = ω y = 0

ω z = 6   r a d / s

As componentes da quantidade de movimento angular, com relação ao ponto O são:

H x = I x ω x - I x y ω y - I x z ω z

H x = 80 ( 0 ) - 72 ( 0 ) - ( - 24 ) ( 6 )

H x = 144   k g ⋅ m 2 / s

H y = - I x y ω x + I y ω y - I y z ω z

H y = - 72 0 - 12 8 0 - ( - 24 ) ( 6 )

H y = 144   k g ⋅ m 2 / s

H z = - I x z �� x - I y z ω y + I z ω z

H z = - - 24 ( 0 ) - ( - 24 ) ( 0 ) + 176 ( 6 )

H z = 1056   k g ⋅ m 2 / s

Logo:

H O = 144 i + 144 j + 1056 k   k g ⋅ m 2 / s

A energia cinética é dada por:

T = 1 2 ω H O

T = 1 2 6 k ⋅ ( 144 i + 144 j + 1056 k )

T = 3168   J

Resposta

H O = 144 i + 144 j + 1056 k   k g ⋅ m 2 / s

T = 3168   J

Ver Outros Exercícios desse livro