Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 4

O tronco de cone é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia I x e expresse o resultado em termos da massa total m do tronco. O tronco tem uma densidade constante ρ .

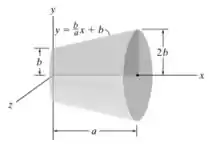
Passo 1

Sabemos que d m = ρ d V , então d m = ρ π y 2 d x = ρ π b 2 a 2 x 2 + 2 b 2 a x + b 2 d x . Vamos integrar o valor da massa para que a gente possa encontrar o valor total da massa. Com isso,

m = ∫ m d m = ρ π ∫ 0 a b 2 a 2 x 2 + 2 b 2 a x + b 2 d x = 7 3 ρ π a b 2

Passo 2

Agora que já conhemos a massa, vamos calcular o valor do momento de inércia. Então,

d I x = 1 2 d m y 2 = 1 2 ρ π y 4 d x

d I x = 1 2 ρ π b 4 a 4 x 4 + 4 b 4 a 3 x 3 + 6 b 4 a 2 x 2 + 4 b 4 a x + b 4 d x

I x = ∫ d I x = 1 2 ρ π ∫ 0 a b 4 a 4 x 4 + 4 b 4 a 3 x 3 + 6 b 4 a 2 x 2 + 4 b 4 a x + b 4 d x = 31 10 ρ π a b 4

Passo 3

Encotramos o valor da massa e do mometo de inércia. Agora basta fazermos um uma jogada matemática para colocar a massa dentro do momento de inércia. Então,

I x = 31 10 ρ π a b 4 = 7 3 ρ π a b 2 93 70 b 2 = 93 70 m b 2

Resposta

I x = 93 70 m b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a aceleração angular do trampolim de 25 kg e as componentes verticais e horizontais da reação no pino A no instante em que o homem realiza o salto. Suponha que a tábua do trampolim seja unif
A barra uniforme de 50 kg está em repouso em uma posição vertical quando a corda fixada a ela em B é submetida a uma força P = 250 N. Determine a aceleração angular inicial da barra e a intensidade da
Inicialmente, a roda A gira no sentido horário com uma velocidade anular constante de ω = 100 rad/s. Se A é colocada em contato com B, que é mantida fixa, determine o número de revoluções antes que a
A barra fina uniforme tem uma massa de 9 kg. Se a mola está distendida quando θ = 0°, determine a intensidade da força reativa exercida sobre a barra pelo pino A quando θ = 45°, se, nesse instante, ω
O disco tem uma massa de 20 kg e está originalmente girando na extremidade da escora com uma velocidade angular ω = 60 rad/s. Se ele é, então, colocado contra a parede, onde o coeficiente de atrito ci