Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 45

A barra fina A B tem uma massa m e está conectada ao apoio por um pino liso em A . O apoio está rigidamente fixado ao eixo. Determine a velocidade angular constante exigida de ω do eixo, a fim de que a barra faça um ângulo de θ com a vertical.

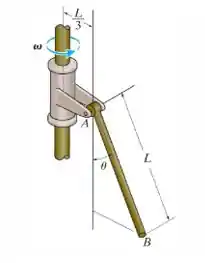
Passo 1

A sistema de rotação xyz é definido com sua origem no centro de massa da haste. Como mostra o dcl abaixo.

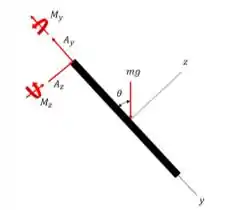
Além disso, o sistema será fixada à haste de modo que sua velocidade angular seja ω e os eixos x ,   y ,   z sempre serão os principais eixos de inércia. Assim, a velocidade angular, conforme mostrado abaixo, é dada por

ω = - ω c o s θ j + ω s e n θ k

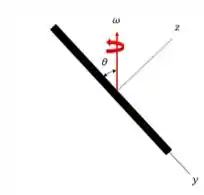
Logo,

ω x = 0

ω y = - ω c o s θ

ω z = ω s e n θ

As acelerações angulares serão nulas. Então,

ω ˙ x = ω ˙ y = ω ˙ z = 0

Passo 2

Os momentos de inércia de massa em x e z são definidos por

I x = I z = 1 12 m L 2

E em y será igual a

I y = 0

Fazendo o somatório dos momentos no eixo x , temos

∑ M x = I x ω ˙ x - I y - I z ω y ω z

- A z L 2 = 0 - 0 - 1 12 m L 2 - ω c o s θ ω s e n θ

Portanto,

Eq. 1:

A z = m ω 2 L 6 s e n θ c o s θ

Passo 3

A aceleração do do centro de massa da haste (mostrado no esquema abaixo) pode ser determinada por

A G = ω 2 r = ω 2 L 2 s e n θ + L 3 = ω 2 L 6 ( 3 s e n θ + 2 )

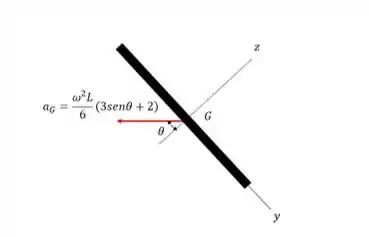
Fazendo o somatório das forças na direção z , temos

∑ F z = m a G z

A z - m g s e n θ = - m ω 2 L 6 3 s e n θ + 2 c o s θ

Eq. 2:

A z = m g s e n θ - m ω 2 L 6 3 s e n θ + 2 c o s θ

Igualando as equações (1) e (2), temos

m ω 2 L 6 s e n θ c o s θ = m g s e n θ - m ω 2 L 6 3 s e n θ + 2 cos ⁡ θ

Logo,

ω = 3 g t a n θ L ( 2 s e n θ + 1 )

Resposta

A velocidade angular de ω , para que a barra faça um ângulo de θ com a vertical, é igua a ω = 3 g t a n θ L ( 2 s e n θ + 1 ) .

Ver Outros Exercícios desse livro