Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 50

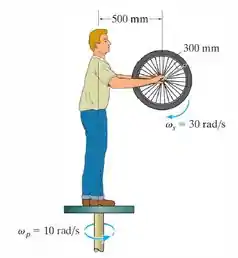
Um homem está parado de pé sobre uma mesa giratória que gira em torno de um eixo vertical com uma velocidade angular constante ω P = 10   r a d / s . Se a roda que ele segura gira com uma velocidade angular constante ω S = 30   r a d / s , determine a intensidade do momento que ele tem de exercer sobre a roda para segurá-la na posição mostrada. Considere a roda como um arco circular fino (anel) tendo uma massa de 3   k g e um raio médio de 300   m m .

Passo 1

O DCL do problema é mostrado abaixo.

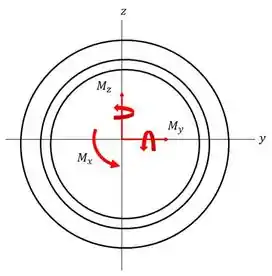
O momento de inércia de massa em y e z serão

I y = I z = 1 2 m L 2 = 1 2 3 0,3 2 = 0,135   k g . m 2

Para o eixo x , teremos

I x = m r 2 = 3 0,3 2 = 0,27   k g . m 2

A velocidade angular da roda é

ω = ω S + ω P = - 30 i + 10 k r a d / s

Assim, a velocidade angular em cada eixo será

ω x = - 30   r a d / s

ω y = 0

ω z = 10   r a d / s

As acelerações angulares são nulas em todos os eixos. Logo,

ω ˙ x =   ω ˙ y = ω ˙ z = 0

Passo 2

Assim, o somatório dos momento na direção x será

∑ M x = I x ω ˙ x - I y Ω z ω y + I z Ω y ω z

M x = 0 - 0 + 0 = 0

Para direção y , temos

∑ M y = I y ω ˙ y - I z Ω x ω z + I x Ω z ω x

M y = 0 - 0 + 0,27 10 - 30 = - 81   N . m

Da mesma forma, para a direção z :

∑ M z = I z ω ˙ z - I x Ω y ω x + I y Ω x ω y

M z = 0 - 0 + 0 = 0

Portanto,

M = M x 2 + M y 2 + M z 2 = 0 2 + - 81 2 + 0 2 = 81   N . m

Resposta

O homem deve exercer sobre a roda um momento de intensidade igual a 81   N . m .

Ver Outros Exercícios desse livro