Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 9

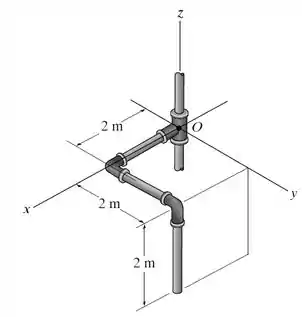
A barra fina tem massa por unidade de comprimento de 6 kg/m. Determine seus momentos e produtos de inércia em relação aos eixos x, y , z.

Passo 1

De acordo com o problema a barra pode ser dividida em 3 segmentos de mesmo comprimento, 2 metros cada. Sabendo que barra fina tem massa por unidade de comprimento de 6 kg/m, temos que :

m 1 = m 2 = m 3 = 6 2 = 12   k g

Passo 2

O momento de inércia I x será:

I x = ∑ I - x ' + m y G 2 + z G 2

I x = 0 + 0 + 1 12 12 2 2 + 12 1 2 + 0 2 + 1 12 12 2 2 + 12 2 2 + ( - 1 ) 2

I x = 80   k g . m 2

O momento de inércia I y será:

I y = ∑ I - y ' + m x G 2 + z G 2

I y = 1 12 12 2 2 + 12 1 2 + 0 2 + 0 + 12 2 2 + 0 2 + 1 12 12 2 2 + 12 2 2 + ( - 1 ) 2

I y = 128   k g . m 2

O momento de inércia I z será:

I z = ∑ I - z ' + m x G 2 + y G 2

I z = 1 12 12 2 2 + 12 1 2 + 0 2 + 1 12 12 2 2 + 12 2 2 + ( 1 ) 2 + 1 12 12 2 2 + 12 2 2 + 2 2

I z = 176   k g . m 2

Passo 3

Devido a simetria o produto de inércia dos eixos que passam pelo centroide dos segmentos são iguais a zero.

O produto de inércia I x y será:

I x y = ∑ I - x ' y ' + m x G y G

I x y = 0 + 12 ( 1 ) ( 0 ) + 0 + 12 ( 2 ) ( 1 ) + 0 + 12 ( 2 ) ( 2 )

I x y = 72   k g . m 2

O produto de inércia I y z será:

I y z = ∑ I - y ' z ' + m y G z G

I y z = 0 + 12 ( 0 ) ( 0 ) + 0 + 12 ( 1 ) ( 0 ) + 0 + 12 ( 2 ) ( - 1 )

I y z = - 24   k g . m 2

O produto de inércia I x z será:

I x z = ∑ I - x ' z ' + m x G z G

I x z = 0 + 12 ( 1 ) ( 0 ) + 0 + 12 ( 2 ) ( 0 ) + 0 + 12 ( 2 ) ( - 1 )

I x z = - 24   k g . m 2

Resposta

De acordo com os passos 1,2 e 3 os momentos e produtos de inércia em relação aos eixos x, y , z da barra fina exposta, são:

I x = 80   k g . m 2

I y = 128   k g . m 2

I z = 176   k g . m 2

I x y = 72   k g . m 2

I y z = - 24   k g . m 2

I x z = - 24   k g . m 2

Ver Outros Exercícios desse livro