Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 22

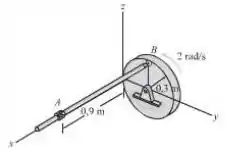
A barra A B de 2   k g está fixada ao disco e ao anel usando juntas esféricas. Se o disco tem uma velocidade angular constante de 2   r a d / s , determine a energia cinética da barra quando ela está na posição mostrada. Suponha que a velocidade angular da barra é direcionada perpendicular ao eixo da barra.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Por definição, temos que:

v A = v B + ω × r A / B  

v A i = - 0,3 2 j + i ω x 0,9 j ω y - 0,3 k ω z - 0,3

v A = - ω y + ω z

2 = ω x + 3 ω z

0 = - ω x - 3 ω y

Resolvendo as equações, temos:

ω x = 0,1818   r a d / s

ω y = - 0,06061   r a d / s

ω z = 0,6061   r a d / s

v A = 0,667   m / s

Temos que:

r A / B = ( 0,9 i - 0,3 j - 0,3 k )

v G = v B + ω × r A / B 2

v G = - 0,3 2 j + i 0,1818 0,9 j     - 0,06061     - 0,3 k 0,6061 - 0,3

v G = 0,333 i - 1 j

v G = 0,333 2 + - 1 2

v G = 1,054

ω = 0,1818 2 + - 0,06061 2 + 0,6061 2

ω = 0,6356   r a d / s

Portanto a parcela de energia será:

T = 1 2 2 1,054 2 + 1 2 1 12 2 3,3166 2 0,6356 2

T = 1,48   N ⋅ m

Resposta

T = 1,48   N ⋅ m

Ver Outros Exercícios desse livro