Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 70
Uma barra de seção transversal quadrada, como indicado, é feita de um aço que é considerado ser elastoplástico com e . Determinar o momento fletor , para que: (a) ocorra o início do escoamento; (b) as zonas plásticas, na parte superior e inferior, da barra tenham de espessura.
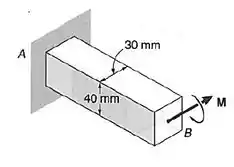
Passo 1
(a) Antes de começar, vamos só fazer uma correçãozinha no enunciado. Ele diz que a barra é de seção quadrada, mas pela figura da questão a seção é retangular. Então vamos considerar essa seção retangular mesmo, tá bem?
O momento fletor no início do escoamento é dado pela fórmulinha:
Como a seção da nossa peça é retangular de lado paralelo ao eixo de rotação com e altura . O momento de inércia fica:
Já que a seção é simétrica, a maior distância entre a linha neutra e um ponto da seção é:
Sabendo que a tensão de escoamento é , já podemos usar nossa fórmulinha:
Passo 2
(b) Queremos o momento para que as zonas plásticas na seção tenham o total de:
Isso significa, que o núcleo elástico deve ter:
Com isso, podemos usar essa fórmulinha para descobrir o momento para esse valor de :
Substituindo tudo o que a gente achou:
Resposta
(a)
(b)