A barra de é suportada por um braço em rotação. O apoio em é um mancal radial, que desenvolve reações normais à barra. O apoio é um mancal axial que desenvolve tanto reações normais à barra quanto ao longo do eixo da barra. Desprezando o atrito, determine as componentes da reação nesses apoios quando o sistema gira com uma velocidade angular constante .
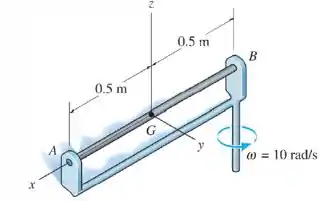
Passo 1
O DCL do problema é mostrado abaixo.
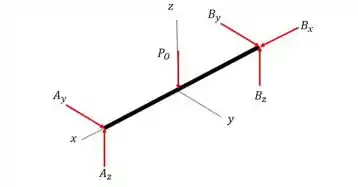
O momento de inércia de massa em e serão
Para o eixo , teremos
As velocidades angulares serão iguais a
E
As acelerações angulares são nulas em todos os eixos. Logo,
Passo 2
Assim, o somatório dos momento na direção será
Para direção , temos
Eq. 1:
Da mesma forma, para a direção :
Eq. 2:
Passo 3
Fazendo o somatório das forças nas três direções, temos
Assim,
Eq. 3:
E
Eq. 4:
Resolvendo o sistema formado pelas equações (2) e (3), obtemos
Similarmente, resolvendo (1) e (4), encontramos
Resposta
Os componentes das reações são: , e .