Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 49
Quatro esferas estão conectadas ao eixo . Se e , determine a massa das esferas e e os ângulos das barras e , de maneira que o eixo esteja dinamicamente equilibrado, isto é, de maneira que os mancais em e exerçam somente reações verticais sobre o eixo na medida em que ele gira. Despreze a massa das barras.
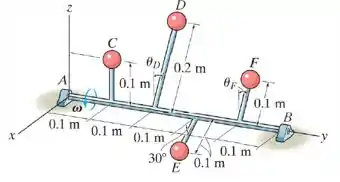
Passo 1
O DCL do problema é mostrado abaixo.
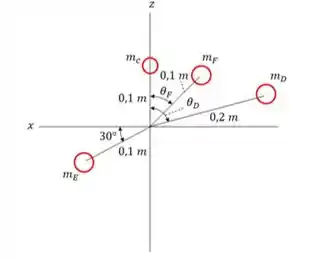
Para
Eq.1:
Para
Eq.2:
Passo 2
Para
Eq. 3:
Para
Eq. 4:
Resolvendo o sistema formado pelas equações (1), (2), (3) e (4), obtemos
Resposta
Portanto, , , e .