Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 118

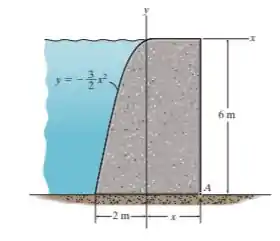
A barragem de concreto por gravidade é projetada de modo que é mantida na posição por seu próprio peso. Determine a dimensão mínima de x de modo que o fator de segurança contra o tombamento em torno do ponto A da barragem seja 2 . O fator de segurança é definido como a razão do momento de estabilização dividido pelo momento de tombamento. As densidades do concreto e da água são ρ c o n c = 2,4 M g m 3   e   ρ w = 1 M g m 3 , respectivamente. Suponha que a barragem não deslize.

Passo 1

Desejamos encontrar o valor mínimo de x dadas as especificações mencionadas no enunciado. Sendo assim, sabemos que na parte parabólica da nossa estrutura nós teremos a força hidrostática agindo, de modo que sua componente vertical consistirá no peso da água nesse “pedaço” da estrutura e será dada por

F v = ρ w ⋅ g ⋅ A ⋅ 1 = 1000 ⋅ 9,81 ⋅ 1 3 ⋅ 2 ⋅ 6 = 39,24 k N

Já a componente horizonta consiste na pressão hidrostática que no nosso caso vai ser representado por uma carga triangular distribuída. Assim, teremos

F h = 1 2 ⋅ ρ w ⋅ g ⋅ h ⋅ 1 ⋅ 6 ≈ 176,58 k N

Passo 2

Agora, o peso da barragem de concreto parabólica é

W c o n c ρ = ρ c o n c ⋅ g ⋅ V = 2400 ⋅ 9,81 ⋅ 2 3 ⋅ 2 ⋅ 6 ⋅ 1 ≈ 188,352 k N

Para a parte retangular teremos

W c o n c r = ρ c o n c ⋅ g ⋅ V = 2400 ⋅ 9,81 ⋅ 6 ⋅ x ⋅ 1 ≈ 141,264 ⋅ x   k N

Passo 3

Por fim, como foi dito no enunciado o nosso fator de segurança F S será dado pela razão do momento de estabilização dividido pelo momento de tombamento, então, teremos

F S = M s M t → 2 = W c o n c ρ ⋅ 3 8 ⋅ 2 + x + W c o n c r ⋅ x 2 + F V ⋅ 3 4 ⋅ 2 + x F h ⋅ 1 3 ⋅ 6 → x ≈ 1,51 m

Resposta

x = 1,51 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine  a intensidade  da  força  hidrostática  atuando  sobre  a  comporta AB,  que  tem  largura  de 0,6 m. O peso específico da água é  p =   9,81   k N / m ³ ³ .
Determine  a intensidade  da  força  hidrostática atuando sobre a comporta AB, que tem largura de  1,5 m. A água tem densidade  p=   1   M g / m ³ ³ .
Determine  a intensidade  da  força  hidrostática  atuando sobre a comporta AB, que tem largura de 2 m.  A água tem densidade  p=   1   M g / m ³ ³ .
Determine  a intensidade  da  força  hidrostática atuando por metro de comprimento da parede. A  água tem densidade  p=   1   M g / m ³ ³.
O fator de segurança para o tombamento da barragem de concreto é definido como a razão entre o momento de estabilização decorrente do peso da barragem e o momento de tombamento em relação a O em virtu