Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 69
O barril de alumínio de cerveja vazio tem uma massa m, centro de massa em G, e raios de giração em relação aos eixos x e y de , e em relação ao eixo z de , respectivamente. Se o barril rola sem deslizar com uma velocidade angular constante, determine seu maior valor sem que a borda A deixe o chão.
Passo 1
Uma vez que o barril rola sem deslizar, o centro instantâneo de velocidade nula está indicado na figura a seguir:
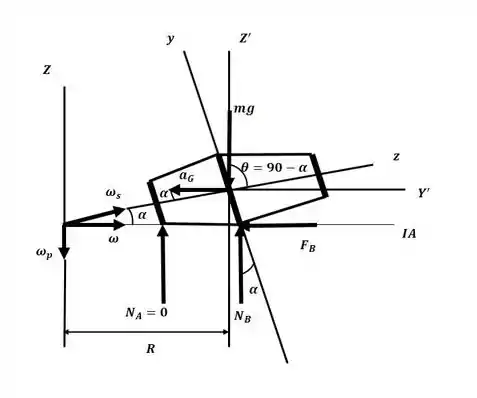
Sendo assim, . Temos ainda que analisar a condição limite onde a borda A está para deixar o châo, por isso .
Uma vez que , e são constantes, o barril gira sobre essa posição fixa. Sendo assim, podemos agora calcular os momentos de inércia do barril:
Passo 2
Com base na figura apresentada no passo 1, agora podemos aplicar a equação de momento para o sistema:
Essa será nossa equação número 1. Uma vez que o centro de massa G do barril gira com relação ao eixo Z da figura apresentada no passo 1, sua aceleração pode ser encontrada fazendo:
Como sabemos também que o centro de massa não se move ao longo do eixo Z’ então:
Passo 3
Agora iremos aplicar o somatório de forças para os eixos Y’ e Z’ ainda com base na figura apresentada no passo 1:
Essa será nossa equação número 2.
Essa será nossa equação número 3. Agora iremos substituir as equações obtidas no passo 3 na nossa equação 1:
Colocando em evidência e isolando os termos, obtemos: