Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 41

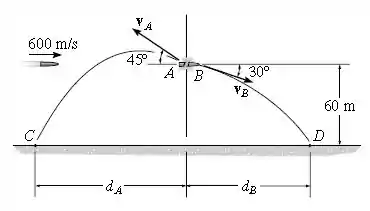
Um projétil de 4   k g viaja a uma velocidade horizontal de 600   m / s , antes de explodir e partir-se em dois fragmentos, A e B , de massas 1,5   k g e 2,5   k g , respectivamente. Se os fragmentos viajam ao longo das trajetórias parabólicas mostradas na figura, determine a intensidade da velocidade de cada fragmento logo após a explosão, e a distância horizontal d B , onde o segmento B atinge o solo em D .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Podemos aplicar conservação de quantidade de movimento:

→ +         m v x = m A v A x + m B v B x

Substituindo os valores, temos:

→ +         4 600 = - 1,5 v A cos ⁡ 45 ° + 2,5 v B cos ⁡ 30 °

2,165 v A - 1,061 v B = 24 00

Analisando em y , temos:

+ ↑         m v y = m A v A y + m B v B y

Substituindo os valores, temos:

+ ↑       0 = 1,5 v A sin ⁡ 45 ° - 2,5 v B sin ⁡ 30 °

v B = 0,8485 v A

Relacionando as duas equações, temos:

v A = 3090,96   m / s

v B = 2622,77   m / s

Passo 2

Agora vamos analisar o movimento de B nas direções y e x .

Para y , temos:

s y = s 0 y + v 0 y t + 1 2 a y t 2

Substituindo os valores, temos:

- 60 = 0 + 2622,77 sin ⁡ 30 ° t B D + 1 2 ( - 9,81 ) t B D 2

4,905 t B D 2 + 1311,38 t B D - 60 = 0

Resolvendo por baskara, encontramos um valor positivo para t B D de:

t B D = 0,04574   s

Para x , temos:

s x = s 0 x + v 0 x t

d B = 0 + 2622,77 cos ⁡ 30 ° 0,04574

d B = 103,91   m

Resposta

v A = 3090,96   m / s

v B = 2622,77   m / s

d B = 103,91   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula de massa m é lançada do ponto A com uma velocidade inicial v0 perpendicular à linha OA e se move sob a ação da força central F dirigida para fora do centro de força O. Sabendo que a part
O disco A gira em um plano horizontal em torno de um eixo vertical a uma taxa constanteθ = 12 r a d / s . O cursor B tem uma massa de 230 g e se movimenta em uma fenda sem atrito aberta no disco. O cu
O pino B de 4 oz desliza ao longo da fenda no braço giratório OC e ao longo da fenda DE de raio b = 20 in que foi aberta em um plano horizontal fixo. Desprezando o atrito e considerando θ = 15r a d /
Um pequeno colar C de 200 g desliza em uma haste semicircular que é colocada para girar sobre a vertical AB a uma taxa constante de 6 rad/s. Determine o valor mínimo requerido do coeficiente de atrito
Foi observado que quando a nave espacial Voyager I alcança o ponto mais próximo do planeta Saturno, sua distância do centro do planeta foi de 185 × 10 3 k m e que tinha uma velocidade de 21 km/s. Sabe