26. Se os blocos e têm peso de cada um, determine o peso do bloco se o comprimento é de . Despreze as dimensões das polias.

Para resolver esse problema temos que sacar que a força que os blocos e fazem nas cordas é a mesma que o ponto sofre na direção da corda, já que tanto de um lado quanto do outra é uma única corda para cada ligação.

Então para achar (peso do bloco E), precisamos usar a condição de que está em equilíbrio, logo:

Mas nessa situação vamos usar apenas na direção , já que em , no obteremos nada de novo.

E para analisar na direção , precisamos das componentes das cordas que sustentam o bloco, nessa direção, mas para fazer isso temos que notar que a força que as cordas e fazem parte de um triângulo retângulo logo podemos achar suas componentes por proporcionalidade dos lados do triângulo. A figura abaixo representa situação de uma das cordas, a outra não precisa porque a análise é exatamente igual.

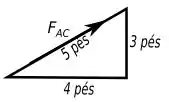
Daí tiramos que a componente de , vale: