Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 48
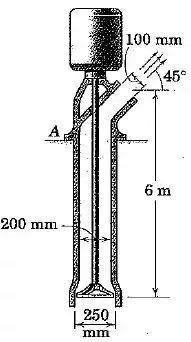
A bomba de sucção possui uma massa líquida de e bombeia água doce contra uma altura de na taxa de . Determine a força vertical entre a base de suporte e o flange da bomba em durante a operação. massa de água na bomba pode ser considerada como a equivalente a um diâmetro de de coluna com de altura.
Passo 1
Muita atenção aqui: essa bomba está pendurada em uma espécie de “penhasco”, e nosso objetivo é calcular a força exercida no suporte da bomba: isso quer dizer que temos que considerar o peso da própria bomba na nossa conta.
Vamos usar a equação para a força resultante em um sistema de escoamento:
Onde o no índice das variáveis indica que estamos falando das suas componentes na direção vertical.
A soma das forças é:
E agora precisamos encontrar relações para a velocidade.
Passo 2
O enunciado já deu o volume de água que é deslocada no sistema por unidade de tempo (), então vamos usar essa relação:
O sistema começa lá embaixo com uma velocidade e uma área circular de diâmetro , então:
E fazendo a mesma coisa para a velocidade com que a água sai na parte de cima:
Mas nós vamos tomar somente a componente de na direção vertical, então:
As outras velocidades e forças já são paralelas à vertical, e não precisam ser projetadas.
Além disso, a taxa de escoamento de massa pode ser calculada a partir de :
Passo 3
Agora vamos substituir tudo na equação que escrevemos no passo :
E podemos calcular a massa de água usando as informações que foram dadas no enunciado:
E substituindo na equação de cima:
Resolvido!
Resposta
A força é .