Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 1.1 - Ex. 6
As três esferas com de diâmetro constrúidas com diferentes metais estão localizadas nos vértices de um triângulo equilátero no espaço profundo. Determine a resultante das forças gravitacionais que as esferas de alumínio e de ferro fundido exercem sobre a esfera de cobre
Passo 1
Vamos começar relembrando a fórmula para o módulo da força gravitacional:
Já temos os valores de , mas precisamos encontrar as massas a partir das densidades dos materiais, que estão na tabela ao final do livro. , , .
E usando a fórmula da densidade e do volume da esfera, e convertendo o raio da esfera para metros, podemos calcular as massas:
Passo 2
Agora já podemos calcular os módulos das forças. Começando com as esferas de Alumínio e Cobre:
E agora as esferas de Ferro e Cobre:
Mas agora, para fazer a soma vetorial dessas duas forças, precisamos achar suas componentes em e . Vamos analisar o ângulo nessa imagem:
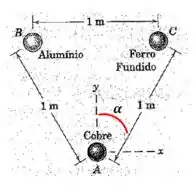
E o ângulo é o mesmo do outro lado!
Passo 3
Agora podemos usar esse ângulo para encontrar os componentes dos vetores:
E fazendo a mesma coisa para a outra força:
E agora a soma fica bem mais simples:
E essa é a força resultante sobre a esfera de alumínio!
Resolvido!
Resposta
A força resultante é .