Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 28

As duas pequenas esferas, cada uma com massa m , estão conectadas por um cordão de comprimento 2 b (medido até os centros das esferas) e estão inicialmente em repouso sobre uma superfície horizontal lisa. Um projétil de massa m 0 com uma velocidade v 0 perpendicular ao cordão atinge-o no meio, provocando a deflexão mostrada na parte b da figura. Determine a velocidade v de m 0 quando as duas esferas quase entram em contato, com θ se aproximando de 90 ° como indicado na parte c da figura. Encontre também θ ˙ para essa condição.

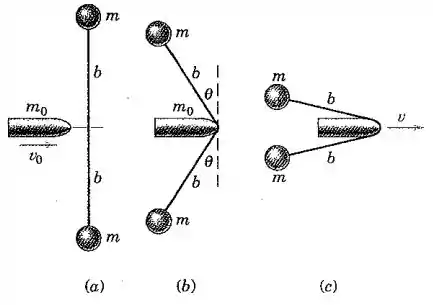
Passo 1

Como há conservação da quantidade de movimento na direção x (mesma direção de v 0 ), temos:

Δ G x = 0

m 0 v + 2 m v - m 0 v 0 = 0

v = m 0 m 0 + 2 m v 0

Passo 2

Além disso, há conservação de energia mecânica, de modo que:

T 1 = T 2

pois nesse caso não há energia potencial. A energia cinética inicial é:

T 1 = 1 2 m 0 v 0 2

Para o cálculo da energia cinética final, há de se considerar que as duas esferas têm tanto a velocidade v (acompanhando o movimento do projétil) como também uma velocidade de rotação, de módulo r θ ˙ = b θ ˙ . Então:

T 2 = 1 2 m 0 v 2 + 2 1 2 m v 2 + b 2 θ ˙ 2

Passo 3

Portanto, fazendo-se T 1 = T 2 , obtemos:

1 2 m 0 v 0 2 = 1 2 m 0 v 2 + 2 1 2 m v 2 + b 2 θ ˙ 2

1 2 m 0 v 0 2 = 1 2 m 0 + 2 m v 2 + m b 2 θ ˙ 2

Lembre-se de que já sabemos a expressão de v e podemos substituir na equação acima:

1 2 m 0 v 0 2 = 1 2 m 0 + 2 m m 0 m 0 + 2 m v 0 2 + m b 2 θ ˙ 2

1 2 m 0 v 0 2 ( m 0 + 2 m ) = 1 2 m 0 2 v 0 2 + m b 2 θ ˙ 2 m 0 + 2 m

m 0 m v 0 2 = m b 2 θ ˙ 2 m 0 + 2 m

θ ˙ = v 0 b m 0 m 0 + 2 m

Resposta

v = m 0 m 0 + 2 m v 0

θ ˙ = v 0 b m 0 m 0 + 2 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade mínima v que a roda deve possuir para conseguir rolar por cima da obstrução. O raio de giração centroidal da roda é k , e se supõe que a roda não deslize.
No conjunto giratório mostrado, o braço O A e a carcaça vinculada do motor B têm uma massa combinada de 4,5k g e um raio de giração em relação ao eixo z de 175m m . A armadura do motor e o disco conec
A esfera homogênea de massa m e raio r é projetada ao longo da inclinação de ângulo θ com uma velocidade inicial v o e sem velocidade angular ( ω o = 0 ) . Se o coeficiente de atrito dinâmico é μ k ,
As três barras estão livres para girar em torno do eixo horizontal fixo x em O . Cada uma das barras A tem uma massa de 20k g , um raio de giração em relação ao eixo x de 300m m , e um centro de massa
A barra esbelta uniforme de massa m e comprimento l tem velocidade angular nula quando a extremidade A bate no chão sem nenhum movimento de retorno. Para um determinado valor da velocidade v 1 pouco a