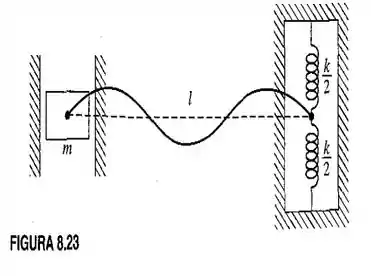
Um cabo de comprimento e massa por unidade de comprimento está esticado sob uma tensao . Uma extrernidade do cabo está ligada a uma massa , que pode se mover dentro de uma fenda desprovida de atrito, e a outra extremidade esta presa a uma mola de rigidez , como mostrado na Figura 8.23. Deduza a equação de frequência para a vibração transversal do cabo.

Com isso, temos que a solução geral será dada por...

Combinando essa equação com a primeira do , temos que...

Substituindo , obtemos que...