Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 22.Problemas - Ex. 9

Um cabo é usado para suspender o cofre de 800   k g . Se o cofre está sendo baixado a 6   m / s quando o motor controlando o cabo subitamente emperra (para), determine a tensão máxima no cabo e a frequência de vibração do cofre. Despreze a massa do cabo e presuma que ele é elático de tal maneira que ele se estende 20   m m quando submetido a uma tensão de 4   k N .

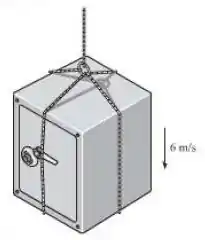
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos que:

k = 4000 0,02 = 200 10 3   N / m

+ ↓ ∑ F y = m a y

m g - k y + y e s t á t i c o = m y ¨

Sabemos que k y e s t á t i c o = m g , logo:

m g - k y - m g = m y ¨

y ¨ + k m y = 0

Temos que p = k m .

p = 200 10 3   800

p = 15,81

Como f = p / 2 π , temos:

f = 15,81 2 π

f = 2,52   H z

Logo:

y ¨ + 2,52 2 y = 0

y ¨ + 250 y = 0

A solução dessa EDO tem a forma:

y = A sin ⁡ p t + B cos ⁡ p t

v = y ˙ = A p cos ⁡ p t - B p sin ⁡ p t

Aplicando as condições iniciais onde:

t = 0

y = 0

v = v 0 = 6

Temos:

0 = A sin ⁡ 0 + B cos ⁡ 0

B = 0   m

E:

6 = A 15,81 cos ⁡ 0 - 0 15,81 sin ⁡ 0

A = 0 , 38   m

A nossa equação será:

y = 0,38 cos ⁡ 15,81 t

A amplitude é dada por:

C = A 2 + B 2

C = 0,38 2 + 0 2

C = 0,38   m

A tensão máxima será:

T m á x = W + k y m á x

T m á x = 800 9,81 + 200 10 3 0,38

T m á x = 83,7   k N

Resposta

f = 2,52   H z

T m á x = 83,7   k N

Ver Outros Exercícios desse livro