Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 28

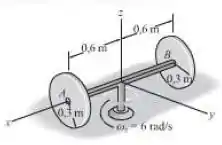
Cada um dos dois discos tem uma massa de 5   k g . O eixo A B tem uma massa de 1,5   k g . Se a montagem gira em relação ao eixo z a ω z = 6   r a d / s , determine sua quantidade de movimento angular em relação ao eixo z e sua energia cinética. Os discos rolam sem deslizar.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Bom... Observando o esquema da figura, podemos notar que quando o eixo z roda, ele faz os discos se movimentarem com uma certa velocidade angular ω x concorda?

Pois bem, conseguimos descobrir essa velocidade angular ω x a partir da geometria do sistema:

Temos:

ω z ω x = 0,3 0,6

ω x = 2 ω z

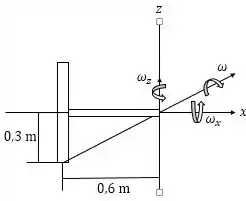
ω x = 12   r a d / s

Com relação aos discos, temos que:

ω A = - 12 i   r a d / s

ω B = 12 i   r a d / s

A quantidade de movimento angular para o eixo z é então:

H z = I d i s c o ω B + I d i s c o ω A + 2 I G A B ω z + I A B ω z

I d i s c o ω B + I d i s c o ω A = 1 2 5 0,3 2 12 i + 1 2 5 0,3 2 - 12 i = 0

H z = 0 + 2 1 4 5 0,3 2 + 5 0,6 2 6 + 1 12 1,5 1,2 2 ( 6 ) k

H z = 24,03   k   k g ⋅ m 2 / s

A Energia cinética é dada por:

T = 1 2 I x ω x 2 + 1 2 I y ω y 2 + 1 2 I z ω z 2

1 2 I x ω x 2 = 1 2 2 1 2 5 0,3 2 12 2

1 2 I x ω x 2 = 32,4

1 2 I y ω y 2 = 0

1 2 I z ω z 2 = 1 2 2 1 4 5 0,3 2 + 5 0,6 2 + 1 12 1,5 1,2 2 6 2

1 2 I z ω z 2 = 72,09

T = 32,4 + 0 + 72,09

T = 104,5   N ⋅ m

Resposta

H z = 24,03   k   k g ⋅ m 2 / s

T = 104,5   N ⋅ m

Ver Outros Exercícios desse livro