Calcule um eixo sólido de aço apoiado em mancais que suporta o rotor de uma turbina no meio. O rotor pesa 500 lb e produz uma potência de 200 hp a rpm. Para manter pequena a tensāo devido ao desequilfbrio do rotor, a velocidade crítica do eixo deve ser um quinto da velocidade de operação do rotor. O comprimento do eixo deve ser igual a no mínimo 30 vezes o seu diâmetro.
Passo 1
Galera temos que Calcular um eixo sólido de aço apoiado em mancais que suporta o rotor de uma turbina no meio. O rotor pesa 500 lb e produz uma potência de 200 hp a rpm.
deslocamento radial estático do eixo sob o peso da turbina
deflexão radial do eixo durante a rotação
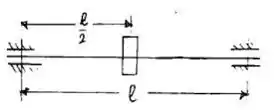
rigidez de carga central viga simplesmente apoiada ou (E1)
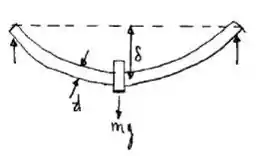
Passo 2
Velocidade crítica: (E2)
Se velocidade crítica da velocidade de operação
(E3)
Em que
E
Passo 3
Para eixo sólido (aço) de diâmetro d e comprimento l, Eq(3) dá:
i.e.,
Deixe em Eq.
E, consequentemente