28. A carga da figura tem massa de e é levantada pelo sistema de polias mostrado. Determine a força na corda em função do ângulo . Faça um gráfico da função da força versus o ângulo para .
Passo 1
Para resolver esse problema temos que sacar que a força de tração na corda é a mesma tração em toda corda, já que tanto de um lado quanto do outra é uma única corda.
Para encontrar o que o enunciado pede, basta assumirmos que o sistema está em equilíbrio, logo temos que:
Então só temos que abrir essas equações para achar a dependência das forças em relação a .
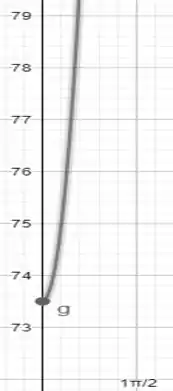
No final teremos o gráfico que o enunciado pede.
Passo 2
Abrindo as equações referente ao equilíbrio do sistema temos:
Logo, nada novo sobre o sol. Vamos para próxima.
Passo 3
Abaixo temos o gráfico pedido no enunciado.