Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 5.4 - Ex. 32
32. O carro esporte tem massa de e centro de massa em . Se as duas molas frontais têm rigidez cada uma e as duas molas traseiras têm cada uma, determine suas compressões quando o carro é estacionado numa ladeira com de inclinação. Que força de fricção deve ser aplicada em cada uma das rodas traseiras para manter o carro parado? Dica: determine primeiro as forças normais em e e, então, determine as compressões nas molas.
Passo 1
Vamos resolver esse problema seguindo a dica do enunciado, vamos achar as força normais em e primeiro e depois lembrando como é dada a força elástica, que é:
Onde é o deslocamento da mola, como já temos o e acharemos , basta isolar o que encontraremos a compressão das molas.
E no meio do caminho iremos achar já que iremos considerar o carro em equilíbrio, para fazer as contas.
Primeiro, vamos ver o diagrama de forças da nossa situação, para analisar as reações que teremos que determinar no nosso sistema e ficar mãos simples de ver o que fazer.
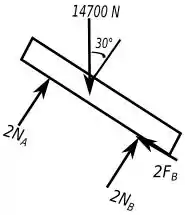
Mas teremos que adotar um sistema de coordenadas diferente que irá nos ajudar nas contas, vamos considerar que o eixo está paralelo a rampa e o eixo perpendicular a mesma.
Então para achar as reações que o enunciado pede, teremos que usar as equações de equilíbrio.
Mas será mais conveniente calcular o momento em relação ao ponto , já quee , não interferem no cálculo do momento pois suas linhas de ação passam por .
Mais uma coisa a ser lembrada é que:
E a força peso é:
Vamos considerar o sentido anti-horário como o positivo.
Passo 2
Vamos então calcular o momento em relação a , para acharmos .
Passo 3
Agora vamos analisar as equações de equilíbrio referentes a força primeiro na direção , depois na direção .
Passo 4
Agora que temos as forças que as molas fazem, podemos achar suas compressões, através do vimos do passo um, então: