Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 175
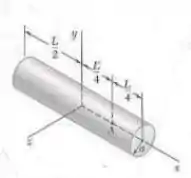
Para o cilindro circular homogêneo mostrado na figura, de raio e comprimento , determine o valor da razão para que o elipsoide de inércia do cilindro seja uma esfera quando calculado no centroide do cilindro, no ponto .
Passo 1
Para no auxiliar na resolução desse problema vamos utilizar como ajuda a figura dada no livro que nos traz a seguinte informação
Dessa imagem tiramos que
A simetria do nosso cilindro implica em . Assim, a partir da equação do elipsoide de inércia vamos encontrar
Para que o elipsoide de inércia seja uma esfera devemos ter que os coeficientes sejam iguais. Portanto,
Passo 2
De forma análoga faremos para quando calculado no ponto . Utilizando o teorema dos eixos paralelos teremos
Assim como fizemos para quando calculado no centroide do cilindro faremos para quando calculado no ponto o que vai implicar em