Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 126

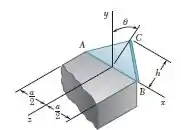
Uma placa delgada triangular de massa m é soldada ao longo de sua base A B a um bloco, tal como mostra a figura. Sabendo que a placa faz um ângulo θ com o eixo y , determine por integração direta o momento de inércia de massa da plca em relação a ao eixo x , b ao eixo y c ao eixo z .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos, primeiramente, definir a equação r para o problema. Considere somente o lado B C do triângulo.

r = h a / 2 x + h

r = h a a - 2 x

A massa do sistema pode ser encontrada por:

m = ρ V

m = ρ t 1 2 a h

m = 1 2 ρ t a h

Em forma diferencial, temos:

d m = ρ t r d x

Passo 2

Para o cálculo do momento de inércia, podemos utilizar o teorema de eixos paralelos.

d I x = 1 12 r 2 d m + r 2 2 d m

d I x = 1 3 r 2 d m

Substituindo d m , temos:

d I x = 1 3 r 2 ρ t r ⋅ d x

Integrando, temos:

I x = 1 12 ρ t a h 3

Passo 3

Como consideramos somente metade do triãngulo, e há simetria nele, podemos duplicar o valor do momento de inércia, sendo assim:

I x = 1 6 ρ t a h 3

Substituindo ρ = 2 m t a h , temos que:

I x = 1 6 m h 2

Passo 4

Para o eixo y ,t emos:

I y = ∫ r y 2 d m

I y = ∫ x 2 + ( r sin ⁡ θ ) d m

Resolvendo, temos que:

I y = m 24 a 2 + 4 h 2 sen 2 ⁡ θ

Passo 5

Para o eixo z , temos:

I z = ∫ r z 2 d m

I z = ∫ x 2 + y 2 d m

I z = ∫ x 2 + r cos ⁡ θ 2 d m

Resolvendo, temos que:

I z = m 24 a 2 + 4 h 2 cos 2 ⁡ θ

Resposta

a ) I x = 1 6 m h 2  

b ) I y = m 24 a 2 + 4 h 2 sen 2 ⁡ θ

c ) I z = m 24 a 2 + 4 h 2 cos 2 ⁡ θ

Ver Outros Exercícios desse livro