Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 166

Determine o momento de inércia do elemento de máquina de aço dos problemas 9.145   e   9.149   em relação ao eixo que passa pela origem e forma ângulos iguais com os eixos x ,   y   e   z .

Passo 1

O elemento de máquina presente nessas duas questões é o seguinte

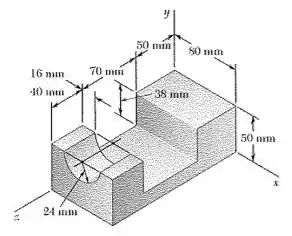
E dos exercícios mencionados no enunciado temos as seguintes informações

I x = 26.4325 ⋅ 10 - 3   k g ⋅ m 2

I y = 31.1726 ⋅ 10 - 3   k g ⋅ m 2

I z = 8.5773 ⋅ 10 - 3   k g ⋅ m 2

I x y = 2.5002 ⋅ 10 - 3   k g ⋅ m 2

I y z = 4.0627 ⋅ 10 - 3   k g ⋅ m 2

I z x = 8.8062 ⋅ 10 - 3   k g ⋅ m 2

Desse problema segue que

λ x = λ y = λ z

Isso implica que

λ x 2 + λ y 2 + λ z 2 = 1 → 3 λ 2 = 1 → λ = 1 3

Passo 2

Podemos, agora, para finalizar o problema vamos substituir na equação que vai nos fornecer o momento de inércia desejado que é dada por

I o l = I x ⋅ λ x 2 + I y ⋅ λ y 2 - 2 I x y ⋅ λ x ⋅ λ y - 2 I y z ⋅ λ y ⋅ λ z - 2 I z x ⋅ λ z ⋅ λ x

I O L = 1 3 ⋅ I x + I y - 2 I x y - 2 I y z - 2 I z x

I O L = 1 3 ⋅ 26.4325 + 31.1726 + 8.5773 - 2 ⋅ 2.5002 + 4.0627 + 8.8062 ⋅ 10 - 3   k g ⋅ m 2

I O L = 11.81 ⋅ 10 - 3   k g ⋅ m 2

Resposta

I O L = 11.81 ⋅ 10 - 3   k g ⋅ m 2

Ver Outros Exercícios desse livro