Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 179

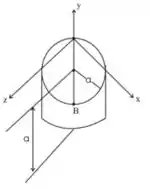
O cilindro circular homogêneo mostrado na figura tem massa m, e o diâmetro OB da sua superfície superior forma ângulos de 45° com os eixos x e z. (a) Determine os momentos principais de inércia do cilindro na origem O. (b) Calcule os ângulos que os eixos principais de inércia em O formam com os eixos coordenados. (c) Esboce o cilindro e mostre a orientação dos eixos principais de inércia em relação aos eixos x, y e z.

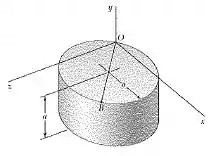
Passo 1

Antes vamos fazer um esboço da vista superior

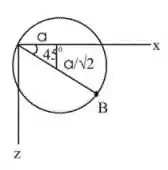
Passo 2

Agora vamos computar os momentos de inércia usando o teorema dos eixos paralelo, temos que

I x = I z = 1 12 m 3 a 2 + a 2 + m a 2 2 + a 2 2 = 13 12 m a 2

I y = 1 2 m a 2 + m a 2 = 3 2 m a 2

Agora observe que os produtos centroides de inércia são zeros por causa da simetria. Então

I x y = I x ' y ' + m x - y - = m a 2 - a 2 =   - 1 2 2 m a 2

I y z = I y ' z ' + m y - z - = m - a 2 a 2 =   - 1 2 2 m a 2

I z x = I z ' x ' + m z - x - = m a 2 a 2 = 1 2 m a 2

Passo 3

Substituindo na eq.

K 3 - I x + I y + I z K 2 + I x I y + I y I z + I z I x - I x y 2 - I y z 2 - I z x 2 K - I x I y I z - I x I y z 2 - I y I z x 2 - I x I x y 2 - 2 I x y I y z I z x = 0

Obtemos

K 3 - 13 12 + 3 2 + 13 12 m a 2 K 2 + 13 12 * 3 2 + 3 2 * 13 12 + 13 12 * 13 12 - - 1 2 2 2 - - 1 2 2 2 - 1 2 2 m a 2 2 K - 13 12 * 3 2 * 13 12 - 13 12 - 1 2 2 2 - 3 2 1 2 2 - 13 12 - 1 2 2 2 - 2 - 1 2 2 - 1 2 2 1 2 m a 2 3 = 0    

Simplificando e como K = m a 2 ζ , obtemos

ζ 3 - 11 3 ζ 2 + 565 144 ζ - 95 96 = 0

Resolvendo

ζ 1 = 0.363383  

ζ 2 = 19 12

ζ 3 = 1.71995

Portanto os momentos principais de inércia são

K 1 = 0.363 m a 2

K 2 = 1.583 m a 2

K 3 = 1.720 m a 2

Passo 4

Para determinar os cossenos diretores λ x ,   λ y , λ z para cada eixo principal, nós usamos as equações

I x - K λ x - I x y λ y - I z x λ z = 0

- I z x λ x - I y z λ y + I z - K λ z = 0  

λ x 2 + λ y 2 + λ z 2 = 1

Substituindo os momentos e os produtos de inercia nas duas primeiras equações temos

13 12 m a 2 - k λ x - - 1 2 2 m a 2 λ y - - 1 2 m a 2 λ z = 0

e

- - 1 2 m a 2 λ x - - 1 2 2 m a 2 λ y + 13 12 m a 2 - K λ z = 0

ou

13 12 - ζ λ x + 1 2 2 λ y - 1 2 λ z = 0           ( 1 )

e

- 1 2 λ x + 1 2 2 λ y + 13 12 - ζ λ z = 0       ( 2 )

Observe que essas equações serão idênticas, de modo que uma precisará ser substituída, se

13 12 - ζ =   - 1 2                         o u                             ζ = 19 12

Assim, uma terceira equação independente será necessária quando a direção dos cossenos associados a K 2 for determinada. Depois para K 1 e K 3 .

Eq. (1) através da Eq. (2), temos

13 12 - ζ - - 1 2 λ x + - 1 2 - 13 12 - ζ λ x = 0

ou

λ z = λ x

Substituindo na Eq. (1)

13 12 - ζ λ x + 1 2 2 λ y - 1 2 λ x = 0

ou

λ y = 2 2 ζ - 7 12 λ x

Substituindo na eq.

λ x 2 + λ y 2 + λ z 2 = 1

Temos

λ x 2 + 2 2 ζ - 7 12 λ x 2 + λ x 2 = 1

ou

2 + 8 ζ - 7 12 2 λ x 2 = 1         ( 3 )

Passo 5

Agora vamos substituir os valores na Eq. (3), para

K1:

2 + 8 0.363383 - 7 12 2 λ x 1 2 = 1        

ou

λ x 1 = λ z 1 =   0.647249

E então

λ y 1 = 2 2 0.363382 - 7 12 0.647249 =   - 0.402662

Assim,

θ x 1 = θ z 1 = 49.7 °                       θ y 1 = 113.7 °

K3:

2 + 8 1.71995 - 7 12 2 λ x 3 2 = 1  

ou

λ x 3 = λ z 3 =   0.284726

E então

λ y 3 = 2 2 1.71995 - 7 12 0.284726 =   0.915348

Assim,

θ x 3 = θ z 3 = 73.5 °                       θ y 3 = 23.7 °

Para o caso K 2 , temos que

- I x y λ x + I y - K λ y - I y z λ z = 0

Substituindo os momentos e os produtos de inercia

- - 1 2 2 m a 2 λ x + 3 2 m a 2 - K λ y - - 1 2 2 m a 2 λ z = 0

ou

1 2 2 λ x + 3 2 - ζ λ y + 1 2 2 λ z = 0

Substituindo o valor de ζ 2 nas equações

13 12 - 19 12 λ x 2 + 1 2 2 λ y 2 - 1 2 λ z 2 = 0

1 2 2 λ x 2 + 3 2 - 19 12 λ y 2 + 1 2 2 λ z 2 = 0

ou

- λ x 2 + 1 2 λ y 2 - λ z 2 = 0

e

λ x 2 - 2 6 λ y 2 + λ z 2 = 0

Resolvendo

λ y 2 = 0

E então

λ y 2 =   - λ x 2

Substituindo na eq.

λ x 2 + λ y 2 + λ z 2 = 1

Temos

λ x 2 2 + λ y 2 2 + - λ x 2 2 = 1

ou

λ x 2 = 1 / 2

λ z 2 =   - 1 2

Portanto

θ x 2 = 45.0 °

θ y 2 = 90.0 °

z 2 = 135.0 °

Passo 6

Para o item C, atente-se que os eixos principais 1 e 3 estão na simetria do plano vertical que passa pelos pontos O e B. O eixo principal 2 está no plano xz.

Resposta

  1.               K 1 = 0.363 m a 2

K 2 = 1.583 m a 2

K 3 = 1.720 m a 2

b )   θ x 1 = θ z 1 = 49.7 °                       θ y 1 = 113.7 °

θ x 2 = 45.0 °

θ y 2 = 90.0 °

z 2 = 135.0 °

θ x 3 = θ z 3 = 73.5 °                       θ y 3 = 23.7 °

Ver Outros Exercícios desse livro