Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 188

Determine o momento de inércia da superfície sombreada em relação aos eixos x e y .

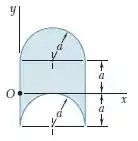
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Podemos dividir a figura nas seguintes seções:

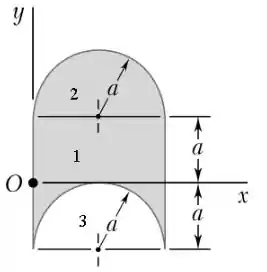
Temos que:

I x 1 = 1 12 2 a 2 a 3

I x 1 = 4 3 a 4

Temos também que:

I A A 2 = I B B 3 = π 8 a 4

Além disso, temos que:

I A A 2 = I - x 2 2 + A d 2

Então:

I - x 2 2 = π 8 a 4 - π 2 a 2 4 a 3 π 2

I - x 2 2 = I - x 3 3 = π 8 - 8 9 π a 4

Passo 2

Portanto, podemos calcular I x 2 e I x 3 agora:

I x 2 = I - x 2 2 + A d 2 2

I x 2 = π 8 - 8 9 π a 4 + π 2 a 2 a + 4 a 3 π 2

I x 2 = 4 3 + 5 π 8 a 4

E:

I x 3 = I - x 3 3 + A d 3 2

I x 3 = π 8 - 8 9 π a 4 + π 2 a 2 a - 4 a 3 π 2

I x 3 = - 4 3 + 5 π 8 a 4

Temos que:

I x = I x 1 + I x 2 - I x 3

Portanto:

I x = 4 3 a 4 + 4 3 + 5 π 8 a 4 - - 4 3 + 5 π 8 a 4

Resolvendo, temos que:

I x = 4 a 4

Passo 3

Agora para y , temos que:

I y 1 = 1 12 2 a 2 a 3 + 2 a 2 2 a 2

I y 1 = 16 3 a 4

Temos também que:

I y 2 = I y 3 = π 8 a 4 + π 2 a 2 a 2

Logo:

I y 2 = I y 3 = 5 π 8 a 4

Temos que:

I y = I y 1 + I y 2 - I y 3

Portanto:

I y = 16 3 a 4 + 5 π 8 a 4 - 5 π 8 a 4

Resolvendo, temos que:

I y = 16 3 a 4

Resposta

I x = 4 a 4

I y = 16 3 a 4

Ver Outros Exercícios desse livro