Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 144

O colar B pode deslizar ao longo da barra AC e é fixado por um pino a um bloco que pode deslizar na fenda vertical como mostrado na figura. Deduza uma expressão da intensidade do binário

Passo 1

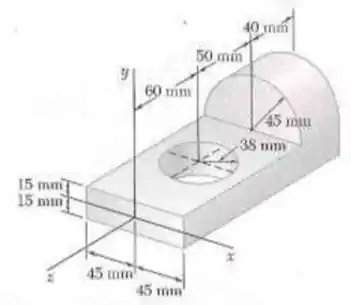
Primeiro, vamos pegar o numero de massa de cada elemento! Vamos considerar como elemento 1 a base com um furo em baixo (consideremos toda a base, inclusive a parte debaixo do semi-circulo). Elemento 2 é o semicírculo em cima da base. E o elemento 3 é justamente o furo! Então, vamos lá! Primeiramente, vamos calcular a massa pela formula da densidade:

m = ρ V

Logo,

m 1 = 7850 0.09 × 0.03 × 0.15 = 3.17925   k g

m 2 = 7850 π 2 × 0.045 2 × 0.04 = 0.99879   k g

m 3 = 7850 π ( 0.038 2 × 0.03 = 1.06834   k g

Passo 2

Agora que temos as massas, vamos aplicar o teorema dos eixos pararelos, para achar os momentos de inercia de massa de cada elemento e soma-los! A figura 9.28 pode auxiliar você para calcular o momento de inercia de massa para os elementos 1 e 3.

I x = I x 1 + I x 2 - I x 3

= 1 12 3.17925 0.03 2 + 0.15 2 + 3.17925 0.075

+ 0.99879   1 4 - 16 9 π 2 0.045 2 + 1 12 0.04 2 + 0.99879 0.13 2 + 4 × 0.045 3 π + 0.015 2  

- 1 12 1.06834   3 0.038 2 + 0.03 2 + 1.06834 0.06

→ I x = 0.0380864   k g ⋅ m 2

Passo 3

Legal galera, a primeira parte da questão já foi! Agora precisamos calcular o raio de giração da nossa peça! É bem tranquilo! Basta usarmos a formula que se usa do momento de inércia no eixo, e a massa da peça!

k x 2 = I x m

Primeiro, vamos calcular o m !

m = m 1 + m 2 - m 3 = 3.17925 + 0.99879 - 1.06834   = 3.10970   k g

Logo,

k x 2 = I x m = 0.0380864 3.10970 → k x = 110.7   m m

Resposta

I x = 0.0380864   k g ⋅ m 2

k x = 110.7   m m

Ver Outros Exercícios desse livro