Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 53
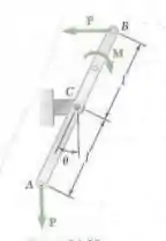
Para a figura a seguir, (a) determine a equação em termo dos dados fornecidos para que o sistema esteja em equilíbrio e (b) determine o valor do ângulo para equilíbrio quando
Passo 1
Fala aí galera, vamos pra mais um problema de estática. O primeiro passo é aplicar as equações de equilíbrio para a barra AB. Pegando o ponto C:
Logo, para equilíbrio.
Passo 2
Agora basta substituir os dados fornecidos e determinar o ângulo que satisfaz a expressão:
Esta expressão não é simples de resolver na mão. Vamos utilizar algum programa, como o Symbolab por exemplo.
Utilizando o programa para resolver esta equação:
Resposta
Exercícios de Livros Relacionados
A estrutura é usada para sustentar o cilindro de 100 kg E. Determine as componentes horizontal e vertical da reação em A e D.
A ponte consiste de três segmentos que podem ser considerados como pinados em A, D e E, sustentados por apoios oscilantes em C e F e sustentados por rolete em B. Determine as componentes horizontal e
3.29. As cordas BCA e CD podem suportar, cada uma, uma carga máxima de 0,5k N . Determine o peso máximo da caixa que pode ser içada em velocidade constante e o ângulo θ para o equilíbrio. Despreze a d
3.33. O fio forma um contorno fechado e passa pelas pequenas polias em A, B, C e D. Se sua extremidade está submetida a uma força de P = 50N , determine a força no fio e a intensidade da força resulta
3.34. O fio forma um contorno fechado e passa pelas pequenas polias em A, B, C e D. Se a força resultante máxima que o fio pode exercer sobre cada polia é 120N , determine a maior força P que pode ser