Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 54

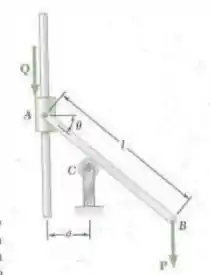
Desprezando o peso da barra AB, determine (a) a equação que deve ser satisfeita quando a haste está em equilíbrio e (b) determine o ângulo para equilíbrio quando P = 64 N ,   Q = 48 N ,   l = 500 m m e a = 125 m m .

Passo 1

Fala aí galera, vamos pra mais um problema de estática. O primeiro passo é aplicar as equações de equilíbrio para a barra AB. Pegando o ponto C:

∑ M C = 0 → Q a = P l - a cos ⁡ θ c o s ⁡ ( θ )

Logo, para equilíbrio.

Q a = P l cos ⁡ θ - P a

Passo 2

Agora basta substituir os dados fornecidos e determinar o ângulo que satisfaz a expressão:

48 × 125 = 64 × 500 × cos ⁡ θ - 64 × 125

cos ⁡ θ = 0,4375

θ = 64,05 º

Resposta

  1. Q a = P l cos ⁡ θ - P a

  2. θ = 64,05 º
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.31. Se a força do rolete liso em B sobre a dobradora de barras precisa ser de 7,5k N , determine as componentes horizontal e vertical da reação no pino A e a intensidade necessária da força F aplica
5.34. Determine as componentes horizontal e vertical da reação no pino A e a força normal na cavilha lisa B sobre o membro.
5.37. A tábua de madeira apoiada entre as construções deflete ligeiramente quando suporta o garoto de 50k g . Essa flexão causa uma distribuição triangular da carga em suas extremidades, tendo intensi
5.38. A mola CD permanece na posição horizontal o tempo todo devido ao rolete em D. Se a mola está descarregada quando θ = 0 ° e o suporte atinge sua posição de equilíbrio quando θ = 30 ° , determine
5.32. A grua é sustentada por um pino em C e um cabo AB. Se uma carga possui massa de 2M g com o seu centro de massa localizado em G, determine as componentes horizontal e vertical da reação no pino C