A coluna é usada para sustentar o piso superior, que exerce uma força de no topo dela. O efeito da pressão do solo na lateral da coluna é distribuído como mostado na figura. Substitua esse carregamento por uma força resultante equivalente e especifique em que ponto a força atua ao longo da coluna, a partir de sua base em .
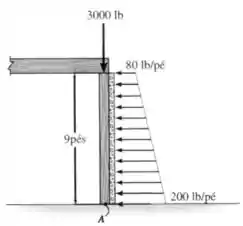
Passo 1
Para encontrar a força total gerada por essa distribuição, primeiro precisamos calcular a área do trapézio na figura:
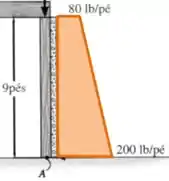
E essa força age na direção horizontal, apontando para a esquerda:
Além disso temos a força de vindo de cima para baixo:
E então a força resultante é:
Passo 2
Podemos especificar esse vetor usando seu módulo e o ângulo que forma com algum semieixo.
E como as duas componentes do vetor são negativas, vamos definir sua direção usando o ângulo que ele forma com o semieixo horizontal negativo no sentido anti-horário:
Passo 3
Agora, para definir o ponto correto de aplicação da nossa força , vamos calcular o momento resultante em relação a .
A força de não produz momento em relação a , porque sua linha de ação passa pelo ponto.
Olhando para as forças geradas pela distribuição, descobrimos que é útil separar em duas partes:
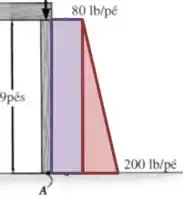
E, para cada área, a sua força associada vai agir na direção do centroide da figura. No caso do quadrado, o centroide está na metade da sua altura, então:
E no caso do triângulo retângulo, o seu centroide tem altura igual a da altura total, quando contanto a partir da parte mais “cheia” do triângulo:
Então o momento total é:
Passo 4
Sabendo qual deve ser o momento resultante, já podemos calcular a posição adequada da força resultante:
Só precisamos considerar a componente horizontal da força, já que a vertical terá momento nulo em relação ao ponto .
Resposta
O carregamento pode ser substituído por uma força de formando um ângulo de com o semieixo horizontal negativo, agindo a da base em .